Question 1202110: https://drive.google.com/file/d/1zsj-S2V9xnu6WYPC88f8xYPvpK_pVFyO/view?usp=sharing
What is the value of x?
Use the rules of special right triangles to find x.
Found 3 solutions by mananth, ikleyn, MathTherapy:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! In Triangle ABC
CB = BA (isoscles triangle) (45-45-90 triangle) each leg = 1/sqrt(2) * hypotenuse
1/sqrt(2) * 6 sqrt(2)
=6
In Triangle BCD (30-60-90) triangle
x = sqrt(3)/2 *6
3sqrt(3)
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
https://drive.google.com/file/d/1zsj-S2V9xnu6WYPC88f8xYPvpK_pVFyO/view?usp=sharing
What is the value of x?
Use the rules of special right triangles to find x.
~~~~~~~~~~~~~~~~~~~
The solution and the answer in the post by @mananth are FATALLY WRONG.
I came to bring a correct solution.
Triangle ABC is a right-angled isosceles triangle.
It has acute angle of 45°; hence, the other acute angle is 45°, too,
and the triangle ABC is isosceles.
Its hypotenuse has the length of  units.
Hence, both its legs, AB and BC, have the same length of 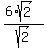 = 6 units.
Triangle BCD is a right-angled triangle.
Its acute angle BCD has the measure of 90° - 60° = 30°.
Its hypotenuse BC is 6 units long, as we found it above.
Hence, x = BD has the length half of the hypotenuse BC, i.e. 6/2 = 3 units,
as the leg opposite to the angle of 30°.
ANSWER. x is 3 units long. x = 3.
Solved.
Answer by MathTherapy(10553)  (Show Source):
You can put this solution on YOUR website!
https://drive.google.com/file/d/1zsj-S2V9xnu6WYPC88f8xYPvpK_pVFyO/view?usp=sharing
What is the value of x?
Use the rules of special right triangles to find x.
The other person apparently has no clue how to do this problem. Plus, his RIDICULOUS answer is WRONG!!
In right ΔABC, ∡CAB = 45o, which makes this triangle a special 45-45-90 right-triangle. Its hypotenuse also measures  .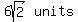
In any 45-45-90 right Δ, the measure of each congruent leg is the right Δ's  .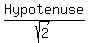
In this case, each congruent leg, AB and BC measures 
In right ΔBCD, ∡CBD = 60o, which makes ∡BCD = 90 - 60 = 30o. This means that ΔBCD is a special 30-60-90 right-triangle.
It's also seen, from above, that its hypotenuse, BC, measures 6 units
Note that side BD is the shorter of ΔBCD's 2 legs, as it's OPPOSITE the smaller of the 2 acute angles (30o & 60o).
In any 30-60-90 right Δ, the length of the shorter leg, knowing hypotenuse, is the  .
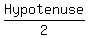In this case, x (or BD), the shorter leg of right ΔBCD measures 
|
|
|
