Question 1202101: It is known that 82% of all new products introduced in grocery stores fail (are taken off the market) within 2 years. If a grocery store chain introduces 61 new products, find the following probabilities. (Round your answers to four decimal places.) Find this on a TI-83
1) within 2 years 47 or more fail
2) within 2 years 58 or fewer fail
3) within 2 years 15 or more succeed
4) within 2 years fewer than 10 succeed
Answer by ikleyn(52890)   (Show Source):
You can put this solution on YOUR website! .
It is known that 82% of all new products introduced in grocery stores fail
(are taken off the market) within 2 years. If a grocery store chain
introduces 61 new products, find the following probabilities.
(Round your answers to four decimal places.) Find this on a TI-83
(1) within 2 years 47 or more fail
(2) within 2 years 58 or fewer fail
(3) within 2 years 15 or more succeed
(4) within 2 years fewer than 10 succeed
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The original problem is, of course, a binomial distribution type.
But the number of trials is great: 61.
In such cases, the traditional approach is not to use the binomial distribution formula.
The traditional approach is to use the normal distribution as an approximation
to the binomial distribution.
This normal distribution has the mean value n*p = 61*0.82 = 50.02 and the
standard deviation 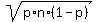 =  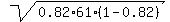= 3.0006 (rounded).
(1) So, in question (1), our goal is to find the area under this normal curve on the right of the
raw mark 47; more precisely, taking the continuity correction factor, on the right
of the raw mark 46.5. You can use regular calculator TI-83
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(46.5, 9999, 50.02, 3.0006).
You get the ANSWER 0.8796 (rounded)
(2) In question (2), our goal is to find the area under this normal curve on the left of the
raw mark 58; more precisely, taking the continuity correction factor, on the left
of the raw mark 58.5. You can use regular calculator TI-83
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(-9999, 58.5, 50.02, 3.0006).
You get the ANSWER 0.9976 (rounded).
(3) "within 2 years 15 or more succeed".
Hence, the rest of the new products, or less than 61-15=46 of the new products, will fail.
P(within 2 years 15 or more succeed) = P(less than 61-15=46 of the new products will fail)
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(-9999, 45.5, 50.02, 3.0006).
The ANSWER is 0.066 (rounded).
(4) "within 2 years fewer than 10 succeed".
Hence, the rest of the new products, or at least 61-10=51 of the new products, will fail.
P(within 2 years fewer than 10 succeed) = P(at least 61-10=51 of the new products, will fail)
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(50.5, 9999, 50.02, 3.0006).
The ANSWER is 0.4365 (rounded).
Solved.
|
|
|
