.
What are the chances that a person who is murdered actually knew the murderer?
The answer to this question explains why a lot of police detective work begins
with relatives and friends of the victim! About 68% of people who are murdered
actually knew the person who committed the murder. Suppose that a detective file
in New Orleans has 59 current unsolved murders. Find the following probabilities
with a TI-83 calculator
1) at least 35 of the victims knew their murderers
2) at most 48 of the victims knew their murderers
3) fewer than 30 victims did not know their murderers
4) more than 20 victims did not know their murderers
~~~~~~~~~~~~~~~~~~~
The original problem is, of course, a binomial distribution type.
But the number of trials is great: 59.
In such cases, the traditional approach is not to use the binomial distribution formula.
The traditional approach is to use the normal distribution as an approximation
to the binomial distribution.
This normal distribution has the mean value n*p = 59*0.68 = 40.12 and the
standard deviation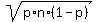 
= 
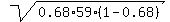= 3.583071308 (rounded).
(1) So, in question (1), our goal is to find the area under this normal curve on the right of the
raw mark 35; more precisely, taking the continuity correction factor, on the right
of the raw mark 34.5. You can use regular calculator TI-83
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(34.5, 9999, 40.12, 3.583071308).
You get the ANSWER 0.9416 (rounded)
(2) In question (2), our goal is to find the area under this normal curve on the left of the
raw mark 48; more precisely, taking the continuity correction factor, on the left
of the raw mark 48.5. You can use regular calculator TI-83
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(-9999, 48.5, 40.12, 3.583071308).
You get the ANSWER 0.9903 (rounded).
(3) "fewer than 30 victims did not know their murderers".
Hence, the rest of the victims, or at least 59-29=30 of the victims, knew their murderers.
P(fewer than 30 victims did not know their murderers) = P(at least 59-29=30 of the victims knew their murderers)
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(29.5, 9999, 40.12, 3.583071308).
The ANSWER is 0.9985 (rounded).
(4) "more than 20 victims did not know their murderers".
Hence, the rest of the victims, or at most 59-20-1=38 of the victims, knew their murderers.
P(more than 20 victims did not know their murderers) = P(at most 59-20-1=38 of the victims knew their murderers)
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(-9999, 38.5, 40.12, 3.583071308).
The ANSWER is 0.3256 (rounded).
Solved.
