|
Question 1202020: You want to have $500,000 when you retire in 10 years. If you can earn 3% interest compounded weekly, how much would you need to deposit now into the account to reach your retirement goal?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the growth rate per time period
1 + r is the growth factor per time period.
n is the number of time periods.
if the annual interest rate is compounded weekly, then:
the time periods are in weeks.
the annual growth rate is divided by 52 to get the growth rate per week.
the number of year is multiplied by 52 to get the number of weeks.
you are given:
p = 100,000
r .03/52 per week.
n = 10 * 52 weeks.
the formula becomes:
f = 100,000 * (1 + .03/52) ^ (52 * 10)
solve for f to get:
f = 134,974.2043 in 520 weeks.
divide 520 weeks by 52 and you get:
f = 134,974.2043 in 10 years.
Answer by ikleyn(52810)  (Show Source):
You can put this solution on YOUR website! .
You want to have $500,000 when you retire in 10 years.
If you can earn 3% interest compounded weekly, how much would you need to deposit now
into the account to reach your retirement goal?
~~~~~~~~~~~~~~~~~~
@Theo got something completely mixed up while reading the problem,
so his solution is incorrect and you better ignore it.
I came to bring you a correct solution.
Use the formula for discretely compounded account
f = p * (1 + r) ^ n
where f is the future value
p is the principal (the deposited amount)
r is the interest rate per time period, presented as a decimal
n is the number of time periods.
Your time periods are weeks.
f = 500000 dollars.
r = 0.03/52.
n = 10 years * 52 = 520 weeks.
Formula becomes 500000 = 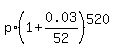 , which gives
p =  = 370441.16 to the nearest cent. ANSWER
Solved.
---------------
To see many other similar (and different) solved problems on compounded interest accounts, look into the lesson
- Compounded interest percentage problems
in this site.
Learn the subject from there and become an expert.
|
|
|
| |
