given tanθ = - 9/4, where 270°≤ θ ≤ 360°:
a) state the other five trigonometric ratios as fractions - show all steps
b determine the value of θ to the nearest degree - show all steps
Since tan θ = 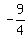 , and 270° ≤ θ ≤ 360°, θ is in the 4th Quadrant,
where sin, csc, tan and cotan are negative (< 0), while and cos and sec are positive (> 0).
, and 270° ≤ θ ≤ 360°, θ is in the 4th Quadrant,
where sin, csc, tan and cotan are negative (< 0), while and cos and sec are positive (> 0).

 Therefore,
Therefore, 
 There are your TRIG. RATIOS! You can now convert each to its nearest-degree measure!!
There are your TRIG. RATIOS! You can now convert each to its nearest-degree measure!!