SOLUTION: I am lost on how to do this problem. I keep confusing myself. arccos(sin(-2pi/3)) arccos(sin(-120), the reference angle is -60 and the sin of -60 = -square root of 3/2. just

I understand, after four tutors trying to help you on that other "arccosine"
problem yesterday, all with different teachings methods, and some arguing over
who has the best teaching method. I'll try again.  I see you think better in
degrees than radians, I'll go that way.

When you ask "What angle between 0 and 360 has such and such trig ratio?" there
are always two angles that could be given as answers.  

However, we want the relationship to be functional, so mathematicians of old had
to define the inverse trig functions so that there would be only ONE answer.  So
they got together and decided to pick one of the two possible values to be the
one and only angle to be the PRINCIPLE inverse trig functional value.  Here is
how they decided to pick it:

First pick the one with the smallest absolute value, whether it's positive or
negative or zero.  Then if it's still a tie as to which one to pick, then pick
the positive one over the negative one.

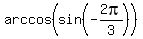 which you changed to 

Let's draw -120. Since it's negative, it goes clockwise from the right side of
the x-axis rotating through -120o.



That's QIII. And the green arc is the reference angle 60o, the
value of the nearest angle to the x-axis, taken positive.

In QIII, the sine is negative so sin(-120o)=

So now the problem 

 becomes



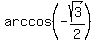Angles have negative cosines in QII and QIII. The two angles that have

 for their cosine have a reference angle of 30o.

That means they are 150o and 210o.

Since 150o is the smaller in absolute value, that's the answer.

However, your teacher probably wants you to change the answer back to
radians. So multiply by 



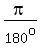
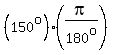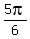Edwin