Question 1201910: cot(arccos-square root 6/3)
I know triangle is in quadrant II because of negative sign.
Just confused on how the answer is -square root 2.
Found 3 solutions by greenestamps, Edwin McCravy, ikleyn:
Answer by greenestamps(13203)   (Show Source): (Show Source):
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hey, see how simple it is:
You just know that 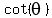 = = 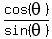 . It is a general formula and general knowledge,
not depending on the given problem.
Concretely in the problem, you are given the cosine: . It is a general formula and general knowledge,
not depending on the given problem.
Concretely in the problem, you are given the cosine:  = = 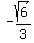 .
All you need now, is to calculate .
All you need now, is to calculate  = +/- = +/-  and then to take the sign of the sine correctly.
After that to make the needed ratio and complete simple arithmetic.
+---------------------------------+
| That's all you need to do. |
| That's all they want from you. |
+---------------------------------+ and then to take the sign of the sine correctly.
After that to make the needed ratio and complete simple arithmetic.
+---------------------------------+
| That's all you need to do. |
| That's all they want from you. |
+---------------------------------+
You are fully instructed.
----------------
For all such problems, the methodology of solution is the same,
and very first and critically important step is to make a 
on the language which you understand
(a) what is given
and
(b) what they want from you.
If you do not make this translation, you will not solve the problem: you simply will not know what to do.
As soon as you make such translation, the solution is easy.
......................
At the beginning, you should not think about details: where some elements/angles are located,
until you understand the major point: what is given and what they want from you.
As soon as you get it, you may start thinking about the details.
|
|
|