|
Question 1201893: Please help me solve this equation: A pebble is dropped into a calm pond, causing ripples in the form of concentric circles. The radius of the outer ripple is increasing at a constant rate of 6 inches per second. When the radius is 4 feet, at what rate (in 1ft/sec) is the total area A of the disturbed water changing.
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please help me solve this  problem. problem.
A pebble is dropped into a calm pond, causing ripples in the form of concentric circles.
The radius of the outer ripple is increasing at a constant rate of 6 inches per second.
When the radius is 4 feet, at what rate (in 1ft/sec) is the total area A
of the disturbed water changing.
~~~~~~~~~~~~~~~~~~~~
About the radius, we know from the problem, that
R = 6*t, where R is in inches and t is the time in seconds.
It is the same as to say that
R =  = =  , where R is in feet and t is the time in seconds.
Hence, the disturbed area in t seconds is
A = , where R is in feet and t is the time in seconds.
Hence, the disturbed area in t seconds is
A =  = =  = =  ft^2. (1)
Then the rate, at which this area is changing, is the derivative of the function (1) over t ft^2. (1)
Then the rate, at which this area is changing, is the derivative of the function (1) over t
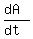 = =  ft^2/s. (2)
The radius R is 4 ft when ft^2/s. (2)
The radius R is 4 ft when
 = 4, or t = = 4, or t =  = 8 seconds.
Substituting t= 8 seconds into (2), we obtain the = 8 seconds.
Substituting t= 8 seconds into (2), we obtain the
 to the problem's question to the problem's question 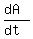 = =  = =  = 4*3.14 = 12.56 ft^2 per second (rounded). = 4*3.14 = 12.56 ft^2 per second (rounded).
Solved, with complete explanations.
-----------------
Notice that the dimension's unit name of the quantity under the question in your post is INCORRECT.
The correct dimension's unit name is ft^2/s, as it is in my solution.
By the way, physicists have a simple criterion whether a person understands a subject or not.
If a person uses wrong dimensions, it is a 100% indication that he (or she) does not understand.
Notice that this your error does not surprise me, since at this forum it is a rare case
and great fiesta, when the post comes in proper form.
|
|
|
| |