SOLUTION: A ball is given an initial velocity of 10.0 m/s at 37° above the horizontal. Assume that the ball landed at the same height. a. Calculate the horizontal and vertical componen

(a)  the horizontal component is   = 10*cos(37°) = 10*0.7986 = 7.986 m/s.

     Horizontal component of velocity remains the same, with no change,
     during the entire flight until landing.


     Vertical component of the initial velocity is 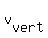  = 10*sin(37°) = 10*0.6018 = 6.018 m/s.



(b)  With the found vertical initial velocity in (a), the algebraic function for the height is

          h(t) = 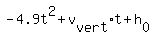 = .    (1)


     Equation to find the time of landing is

           = .


     After canceling    in both sides, this equation takes the form

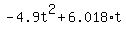           = 0,

          (-4.9t + 6.018)*t = 0

     and gives the value for the time of landing  t = 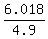 = 1.228 of a second.


     So, the ball flights during 1.228 seconds.



(c)  Half of this time, 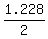  = 0.614 of a second, the ball is on ascending trajectory.

     Second half, or 0.614 of a second, the ball is on descending trajectory.


     To find the range (the horizontal distance), multiply the horizontal component of the velocity 
     by the flight time

         the range = 7.986*1.228 = 9.807 m (rounded).


     To find the maximum height, find the maximum of this quadratic function (1)  (see above).

     As I just said, during 0.614 of a second the ball moves up, so substitute t= 0.614 s
     into the function.


     Doing this way, you will find the maximum height over 

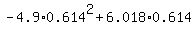          =  = 1.85 m  (rounded).