Question 1201843: In the figure below, ADC is a chord of a circle centre O and passing
through the points A, B and C. BD is a perpendicular bisector
of the chord AC. AD=8 cm and BD=2 cm. Calculate the area of the
minor segment ABCD.

Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One and ONLY ONE problem/question per post.
It is the RULE, the POLICY and the REQUIREMENT of this forum.
It is written in this page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems.
It is assumed that you read these rules before posting.
It is also assumed that you do understand what is written in that page and follow the rules.
Those who violate them, work against their own interests.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In the figure below, ADC is a chord of a circle centre O and passing
through the points A, B and C. BD is a perpendicular bisector
of the chord AC. AD=8 cm and BD=2 cm. Calculate the area of the
minor segment ABCD.
I'll just do the first one for you.
Here are the steps to find the area of a segment of a circle.
1. Identify the radius of the circle and label it 'r'.
2. Identify the central angle AOC made by the arc of the segment and label it
 .
3. Find the area of triangle AOC using the formula .
3. Find the area of triangle AOC using the formula  or or  .
4. Find the area of the sector OABC using the formula .
4. Find the area of the sector OABC using the formula
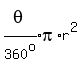 , if θ is in degrees (or) , if θ is in degrees (or)
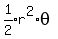 , if θ is in radians.
5. Subtract the area of the triangle OAC from the area of the sector OABC to
find the area of the segment ABCD.
So we need to find radius r and angle θ. , if θ is in radians.
5. Subtract the area of the triangle OAC from the area of the sector OABC to
find the area of the segment ABCD.
So we need to find radius r and angle θ.
 Draw in OD (in green). Since OA, OB, OC are all radii, with length r,
and since BD=2 cm, OD = OB-BD = r-2
Draw in OD (in green). Since OA, OB, OC are all radii, with length r,
and since BD=2 cm, OD = OB-BD = r-2
 To find radius r, we use the Pythagorean theorem on right triangle OAD:
To find radius r, we use the Pythagorean theorem on right triangle OAD:
 To find θ, we use:
To find θ, we use:


 Now we go back to the given figure:
Now we go back to the given figure:
 For step 3, we find the area of triangle OAC either by
For step 3, we find the area of triangle OAC either by

 or
or  .
For step 4, we find the area of the entire sector ABCO either by .
For step 4, we find the area of the entire sector ABCO either by
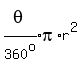 , if θ is in degrees , if θ is in degrees
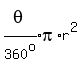 ^""/360^o)*pi*r^2}}} ^""/360^o)*pi*r^2}}} 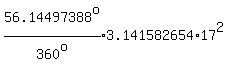  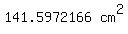 (or)
(or)
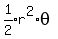 , if θ is in radians. , if θ is in radians.
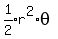  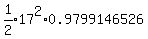  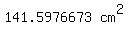 Notice there's a slight difference between those two values.
Finally we do step 6 and subtract the area of the triangle from the area of the
sector
Notice there's a slight difference between those two values.
Finally we do step 6 and subtract the area of the triangle from the area of the
sector
 (or)
(or)
 Edwin
Edwin
|
|
|