SOLUTION: This is a factoring word problem when you have to use the property of zero. The problem says "A garden that is 4 meters wide and 6 meters long is to have a uniform border such that

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: This is a factoring word problem when you have to use the property of zero. The problem says "A garden that is 4 meters wide and 6 meters long is to have a uniform border such that      Log On


   

Question 120184: This is a factoring word problem when you have to use the property of zero. The problem says "A garden that is 4 meters wide and 6 meters long is to have a uniform border such that the area of the border is the same as the area of the garden. Find the width of the border.Could you please help me?
Found 2 solutions by Earlsdon, solver91311:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
First, the area of the garden A%5Bg%5D is:
A%5Bg%5D+=+6%2A4=24sq.m
The total area A%5Bt%5D of the garden plus the surrounding border is:
A%5Bt%5D+=+%286%2B2x%29%284%2B2x%29 where x is the width of the uniform border.
Since the area of the border is to equal the area of the garden, we need to find the area of the border alone, which is:
A%5Bt%5D+-+A%5Bg%5D and this is to equal the area of the garden A%5Bg%5D, so...
A%5Bt%5D-A%5Bg%5D+=+A%5Bg%5D or...
A%5Bt%5D-2A%5Bg%5D+=+0 Let's find A%5Bt%5D
A%5Bt%5D+=+%286%2B2x%29%284%2B2x%29
A%5Bt%5D+=+24%2B20x%2B4x%5E2 and the area of the garden, A%5Bg%5D+=+6%2A4 or:
A%5Bg%5D+=+24 Now we'll subtract:
A%5Bt%5D-2A%5Bg%5D+=+0
4x%5E2%2B20x%2B24-2%2824%29+=+0
4x%5E2%2B20x-24+=+0 Factor out a 4 to simplify calculations.
4%28x%5E2%2B5x-6%29+=+0 so that...
x%5E2%2B5x-6+=+0 Solve this quadratic equation by factoring.
%28x-1%29%28x%2B6%29+=+0 Apply the zero product principle:
x-1+=+0 or x%2B6+=+0
If x-1+=+0 then x+=+1 or
If x%2B6+=+0 then x+=+-6
So the two solutions to the quadratic are:
x+=+1 This is a valid solution because the width, x, has to be a positive value.
x+=+-6 This solution is not valid as the width, x, cannot be a negative value.
The border is 1 meter wide.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
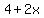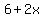Let's say that the width of the border is x. Then the overall width of the garden and its border on both sides must be 4%2B2x. Likewise, the overall length must be 6%2B2x. See the diagram.



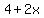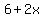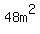So the dimensions of the outer edge of the border are 4%2B2x by 6%2B2x. Since the area of the garden is 4%2A6=24m%5E2, and the area of the border has to be equal to that, the overall area of the garden and the border must be 2 times the area of the garden or 48m%5E2. But the overall area is also given by its length times its width, so we can write:

%284%2B2x%29%286%2B2x%29=48

Use FOIL:

24%2B20x%2B4x%5E2=48

Put into standard form:

4x%5E2%2B20x-24=0

Divide by 4:

x%5E2%2B5x-6=0

Factors of -6 that add to +5 are 6 and -1, so:

%28x-1%29%28x%2B6%29=0

%28x-1%29%28x%2B6%29=0 if and only if x=1 or x=-6, but you can exclude x=-6 because we are looking for a length measurement.

Therefore x=1m

Check:
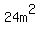The outside dimensions of the border must be 4%2B2%2A1=6 by 6%2B2%2A1=8 and the overall area must be 6%2A8=48m%5E2. Subtract the area of the original garden, 24m%5E2, and the area of the border is 48-24=24m%5E2. All conditions of the problem are met: The border is uniform, that is it is 1 meter wide on all sides, and the area of the border is equal to the area of the garden. Answer checks.

Hope that helps,
John