|
Question 1201828: water is flowing through a pipe with radius 14 cm.The maximum depth of the water is 9 cm.What is the width,PQ,of the surface of the water?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer:
6*sqrt(5) centimeters exactly
6*sqrt(5) = 13.4164078649987 centimeters approximately
Round that approximate value however needed.
Work Shown:
This is what the diagram probably looks like

The diagram is not to scale.
The radius 14 cm is broken down into the pieces 5 cm and 9 cm.
The water's height is 9 cm, and the remaining 5 cm is the gap from the water line to the center of the circle.
The radius bisects the chord, meaning each smaller congruent piece is x cm long.
Apply the intersecting chords theorem
https://www.mathsisfun.com/geometry/circle-intersect-chords.html
and we get the following
a*b = c*d
x*x = 9*5
x^2 = 9*5
x = sqrt(9*5)
x = sqrt(9)*sqrt(5)
x = 3*sqrt(5)
Therefore,
2x = 2*3*sqrt(5) = 6*sqrt(5) represents the exact width of the water's surface when the max depth of the water is 9 cm.
6*sqrt(5) = 13.4164078649987 approximately.
Edit: I just realized I made a silly error. Refer to the solution by @ikleyn for the correct values to use in the intersecting chords theorem.
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
water is flowing through a pipe with radius 14 cm.The maximum depth of the water is 9 cm.
What is the width, PQ, of the surface of the water?
~~~~~~~~~~~~~~~~~~~
The solution by @math_tutor2020 is INCORRECT.
The error is in incorrect using the intersecting chords theorem.
I came to bring a correct solution.
My solution is in two different forms, for better clarity.
Solution 1
In the post by math_tutor2020, you can see the right-angled triangle
with the hypotenuse of 14 cm (the radius from the center to the point P or Q)
and one leg of 14-9 = 5 cm.
Hence, half of PQ is  = =  = = 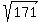 .
Then the segment PQ itself is .
Then the segment PQ itself is  = 26.1534 cm (rounded) ANSWER
Solution 2
You can apply the intersecting chords theorem - but you should to use it in correct way.
Then two parts of the horizontal chord are x cm each,
while two parts of the vertical chord are 9 cm and 5+14 = 19 cm.
The intersecting chords theorem takes the form
x*x = 9*19, or x^2 = 171, x = = 26.1534 cm (rounded) ANSWER
Solution 2
You can apply the intersecting chords theorem - but you should to use it in correct way.
Then two parts of the horizontal chord are x cm each,
while two parts of the vertical chord are 9 cm and 5+14 = 19 cm.
The intersecting chords theorem takes the form
x*x = 9*19, or x^2 = 171, x = 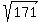 , PQ = 2x = , PQ = 2x =  = 26.1534 cm (rounded) ANSWER
giving the same number. = 26.1534 cm (rounded) ANSWER
giving the same number.
Solved.
-----------------
On the intersecting chords theorem, see the lesson
- The parts of chords that intersect inside a circle,
in this site.
|
|
|
| |