Question 1201705: A 45-45-90 triangle is joined with a 30-60-90 triangle with a hypotenuse of 24 for the 30-60-90 triangle. Find the other 3 sides.
Found 4 solutions by josgarithmetic, Edwin McCravy, ikleyn, mccravyedwin:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! One way to draw this is that the hypotenuse of the 30 30 90 triangle is one of the legs of the 45 45 90 triangle.
The other leg of the 45 45 90 triangle is also 24 units, and the hypotenuse of this triangle is 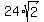 . .
You could use Pythagorean Theorem formula for the other special triangle's legs. Recognize that the short leg is 12 units, hypotenuse is 24 (given), and.....
 . .
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We are not told which way the 30-60-90 triangle is turned. So there are two
solutions.
A 45-45-90 triangle is half of a square cut down its diagonal.
A 30-60-90 triangle is half of an equilateral triangle cut through a vertex
perpendicular to the opposite side.
The properties of all 45-45-90 triangles are:
1. the two legs are equal
2. the hypotenuse is  times the length of a leg.
The properties of all 30-60-90 triangles are:
1. the shorter leg is half of the hypotenuse.
2. the longer leg is times the length of a leg.
The properties of all 30-60-90 triangles are:
1. the shorter leg is half of the hypotenuse.
2. the longer leg is  times the shorter leg.
First solution (below):
Since the hypotenuse BC of triangle BCD is 24, its shorter leg, CD, is half of
24, or 12.
Since the shorter leg CD is 12, the longer leg BD is times the shorter leg.
First solution (below):
Since the hypotenuse BC of triangle BCD is 24, its shorter leg, CD, is half of
24, or 12.
Since the shorter leg CD is 12, the longer leg BD is  .
Since leg CD of triangle ACD is 12, the other leg AD is also 12, and the
hypotenuse AC is .
Since leg CD of triangle ACD is 12, the other leg AD is also 12, and the
hypotenuse AC is  .
So .
So  and AB = and AB = 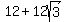
 Second solution (drawn below):
Since the hypotenuse BC of triangle BCD is 24, its shorter leg, BD, is half of
24, or 12.
Since the shorter leg BD is 12, the longer leg CD is
Second solution (drawn below):
Since the hypotenuse BC of triangle BCD is 24, its shorter leg, BD, is half of
24, or 12.
Since the shorter leg BD is 12, the longer leg CD is  .
Since leg CD of triangle ACD is .
Since leg CD of triangle ACD is  , the other leg AD is also , the other leg AD is also
 , and the hypotenuse AC is , and the hypotenuse AC is  times times 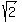 .
So .
So  and AB = and AB = 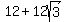
 Edwin
Edwin
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As this problem is worded, printed, posted and presented, I do not understand, at all, what is about.
This combination of words "a triangle is joined with other triangle" is not a canonical term
and has no a uniquely defined meaning in Math.
Edwin counted two ways to joint the given triangles by joining their legs.
There is third way to join triangles by joining their hypotenuses.
In addition, there are several other ways to join triangles by joining a leg of one triangle and the hypotenuse of the other triangle.
Also, the words "joining triangles" does not necessary mean that the triangles' sides are congruent in any combination.
So, my impression that this "problem" is composed by a person who is unprofessional in writing Math problems,
but is more inclined to writing essays.
Writing Math and writing essays are two very different styles (like classic music and jazz are different styles),
and I do not advise to mix these styles, if you want other people understand you and do not laugh quietly to the side.
To the future generations of students, who, probably, will read this post,
my advise is do not consider this problem seriously. Simply ignore it - as if you never saw it.
//////////////////
As an entertainment problem, it is, probably, not so bad.
If to consider it as entertainment problem, then the solution should be separated in parts.
Part 1. In 30-60-80 triangle the hypotenuse is 24 units long.
Find the legs.
Part 2. In 45-45-90 triangle one leg is 24 units.
Find the other leg and the hypotenuse.
Part 3. In 45-45-90 triangle the hypotenuse is 24 units.
Find the legs.
And several other similar parts.
The solution to each part is more than obvious.
Than more I submerge in this problem, than better I see that it is a perfect way
to kill time for nothing, without any sense and without learning anything/nothing useful.
For young mind my advise is - keep away from this task; run out as fast as you can.
\\\\\\\\\\\\\\\\\\\
Edwin, if you read my post attentively, you will see that my pathos is directed
not against "the student" and not against your solution.
I highly appreciate your knowledge and your wisdom, your participation and your contribution in this forum.
My pathos is directed against those "writers", who try to compose Math problems
and to disseminate them, without having adequate skills writing Math.
The number of such people in nova days is million (if not 100 millions).
They all do not know Math and can not express any single Math statement correctly.
But they all want to be Math teachers and all want to teach others.
Answer by mccravyedwin(408)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We should not always blame the student for stating problems ambiguously.
Teachers are also often guilty. Also to be exactly precise in English sometimes
requires so many words it bogs the problem down. I think the most likely way
someone would take 'to join two right triangles" is tp put their right
angles together as a linear pair, since the right angles are the only MEASUREMENT
they automatically have in common.
|
|
|