SOLUTION: If s is inversely proportional to the square root of t , than if s=28 and t=64 , find: a) S when t=81 b) t when s=60 28=k/√64 and therefore k=224 a) I have no difficu

Algebra ->  Test -> SOLUTION: If s is inversely proportional to the square root of t , than if s=28 and t=64 , find: a) S when t=81 b) t when s=60 28=k/√64 and therefore k=224 a) I have no difficu      Log On


   

Question 1201676: If s is inversely proportional to the square root of t , than if s=28 and t=64 , find:
a) S when t=81
b) t when s=60
28=k/√64 and therefore k=224
a) I have no difficulty in letter a (s=224/√81=24.9) but ..
b) 60=224/√t
t=√(224/60)=1.93
But the answer on my book is 13.94 (letter b )
How is letter b worked out ?
Found 3 solutions by mananth, MathTherapy, greenestamps:
Answer by mananth(16946) About Me  (Show Source):
You can put this solution on YOUR website!
60=224/√t
sqrt%28t%29+=%28224%2F60%29=3.73
squaring
t = (3.73)^2= 13.93

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
If s is inversely proportional to the square root of t , than if s=28 and t=64  , find: 
a) S when t=81
b) t when s=60 

28=k/√64  and therefore k=224

a) I have no difficulty in letter a  (s=224/√81=24.9) but ..

b)  60=224/√t
     t=√(224/60)=1.93
But the answer on my book is  13.94  (letter b ) 
How is letter b  worked out ?

s is inversely proportional to the square root of t, so that gives us: matrix%281%2C3%2C+s%2C+%22=%22%2C+k%2Fsqrt%28t%29%29, so "28 = k/√64" is CORRECT,
and therefore k = 224 (8 * 28)

a) I have no difficulty in letter a  (s=224/√81=24.9) but ..

b) t when s=60 

b)  60 = 224/√t
     t = √(224/60)=1.93 <==== This is where you're WRONG!. I think you got a little confused.
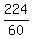You seem to have taken the square root of 224%2F60 instead of SQUARING it! You need to APPLY the INVERSE
operation here, and the INVERSE of taking the square root is squaring!

In other words, matrix%281%2C3%2C+60%2C+%22=%22%2C+224%2Fsqrt%28t%29%29
              matrix%281%2C3%2C+60sqrt%28t%29%2C+%22=%22%2C+224%29 ------- Cross-multiplying
                matrix%281%2C3%2C+sqrt%28t%29%2C+%22=%22%2C+224%2F60%29
             matrix%281%2C3%2C+%28sqrt%28t%29%29%5E2%2C+%22=%22%2C+%28224%2F60%29%5E2%29 ---- Squaring BOTH sides
                  

NEVER, EVER, EVER, EVER round prematurely like the other person did! Most times when you do, your answer will be
different from the correct answer! Furthermore, he's still WRONG, since matrix%281%2C3%2C+3.73%5E2+%3C%3E+%2213.93%2C%22%2C+nor%2C+13.94%29

Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


In most textbooks or other references, s being inversely proportional to the square root of t would be described by introducing a proportionality constant k and using the equation s=k%2Fsqrt%28t%29.

In practice, it is nearly always easier to think in terms of the product of s and the square root of t being constant.

So with the given information that s is 28 when t is 64, we have

s%2Asqrt%28t%29=28%2Asqrt%2864%29=28%2A8=224

So however s or t changes, the product of s and the square root of t will always be 224.

So....

a) find S when t is 81:

S%2Asqrt%2881%29=224
9S=224
S=224%2F9

b) find t when s is 60:

60%2Asqrt%28t%29=224
sqrt%28t%29=224%2F60=56%2F15
t=%2856%2F15%29%5E2=3136%2F225 = 13.94 rounded to 2 decimal places.

The other tutor pointed out that your error in part b was taking a square root when you should have been squaring. You are far less likely to make that kind of error if you work inverse variation problems in the manner described above.