Question 1201656: If (-1,3,5) x (0,a,1) = (-2,1,-1), determine a
This is from my 'cross product' lesson under vectors. Thank you.
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If (-1,3,5) x (0,a,1) = (-2,1,-1), determine a
This is from my 'cross product' lesson under vectors. Thank you.
~~~~~~~~~~~~~~~~~~
The cross-product works this way
(-1,3,5) x (0,a,1) = det  In the right side i, j, and k are the unit vectors along x-, y- and z-coordinate axis.
Let's consider x-component of the cross-product.
According to the rules of calculating this determinant, we should cross it out the first line and first row
in this matrix and calculate the determinant of the remaining 2x2-matrix
det
In the right side i, j, and k are the unit vectors along x-, y- and z-coordinate axis.
Let's consider x-component of the cross-product.
According to the rules of calculating this determinant, we should cross it out the first line and first row
in this matrix and calculate the determinant of the remaining 2x2-matrix
det 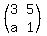 = 3*1 - 5*a = 3 - 5a.
It should be equal x-coordinate of the vector (-2,1,-1), which is -2.
It gives us this equation
3 - 5a = -2.
It is easy to solve
3 + 2 = 5a
5 = 5a
a = 5/5 = 1.
ANSWER. a = 1. = 3*1 - 5*a = 3 - 5a.
It should be equal x-coordinate of the vector (-2,1,-1), which is -2.
It gives us this equation
3 - 5a = -2.
It is easy to solve
3 + 2 = 5a
5 = 5a
a = 5/5 = 1.
ANSWER. a = 1.
Solved, with explanations.
|
|
|