Question 1201599: Find the exact values of sin 2𝜃, cos 2𝜃, and tan 2𝜃 for the given value of 𝜃.
cot 𝜃 = 3/4;180° < 𝜃 < 270°
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the exact values of sin 2a, cos 2a, and tan 2a for the given value of a.
cot(a) = 3/4;180° < a < 270°.
~~~~~~~~~~~~~~~~~
Since 180° < a < 270°, angle "a" is in the 3rd quadrant, QIII.
From the definition of the cot-function, it is the ratio of the attached leg to the opposite leg.
So, the attached leg to angle "a" of the right angled triangle is 3 units long horizontally, opposite to x-axis;
the opposite leg to angle "a" of the right angled triangle is 4 units long vertically, opposite to y-axis.
The hypotenuse is 5 units long ( 5 = 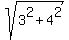 = =  ).
Hence, sin(a) = ).
Hence, sin(a) = 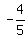 ; cos(a) = ; cos(a) =  . The signs are "-", because we are in QIII.
Therefore
sin(2a) = 2*sin(a)*cos(a) = . The signs are "-", because we are in QIII.
Therefore
sin(2a) = 2*sin(a)*cos(a) = 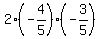 = = 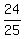 .
cos(2a) = .
cos(2a) =  = = 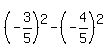 = = 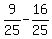 = = 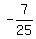 .
By the way, it means that angle "2a" is in QII.
Next, tan(2a) = .
By the way, it means that angle "2a" is in QII.
Next, tan(2a) =  = = 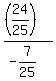 = = 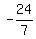 . .
Solved.
|
|
|