Question 1201576: 116.6% of the work done by B at 10% of his efficiency is equal to
25% of the work done by A when he work at 75% more than his
efficiency. Both A and B working together can complete the work in 6
days. Find the time taken by B to complete the whole work ?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Suppose A can do 1 job in x days at 100% efficiency, so his work rate is 1/x
jobs per day.
B can do 1 job in y days at 100% efficiency, so his work rate is 1/y jobs per
day
>>>Both A and B working together [at 100% efficiency] can complete the work in
6 days.<<<
 At 10% [
At 10% [ ] 1efficiency, B's work rate is ] 1efficiency, B's work rate is 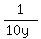 jobs per day.
At 75% [ jobs per day.
At 75% [ ] more than his efficiency, A's work rate is 175% [ ] more than his efficiency, A's work rate is 175% [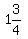 or
or  ]
or ]
or  jobs per day.
>>>116.6% of the work done by B at 10% of his efficiency<<<
That means in any given amount of time, say 1 unit of time, so it says
116.6% of the work done by B at 10% of his efficiency in 1 unit of time:
[I'm going to consider that as 116.6666666...% or jobs per day.
>>>116.6% of the work done by B at 10% of his efficiency<<<
That means in any given amount of time, say 1 unit of time, so it says
116.6% of the work done by B at 10% of his efficiency in 1 unit of time:
[I'm going to consider that as 116.6666666...% or  or
or  , to avoid god-awful decimals or fractions.]
That's , to avoid god-awful decimals or fractions.]
That's 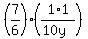 , or , or  >>>is equal to<<<
>>>25% [1/4] of the work done by A when he works at 75% more than his
efficiency.<<<
That means in the same amount of time, say 1 unit of time, so it says
So
>>>is equal to<<<
>>>25% [1/4] of the work done by A when he works at 75% more than his
efficiency.<<<
That means in the same amount of time, say 1 unit of time, so it says
So  of A's work rate at of A's work rate at 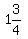   That's
That's  jobs per day.
So we have the equation jobs per day.
So we have the equation




 Substitute in
Substitute in

 Multiply the first term by
Multiply the first term by 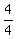



 Multiply through by 5/38
Multiply through by 5/38
 Take reciprocals
Take reciprocals

 <--- Answer: B can do 1 job in 7.6 days.
Edwin <--- Answer: B can do 1 job in 7.6 days.
Edwin
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
116.6% of the work done by B at 10% of his efficiency is equal to
25% of the work done by A when he work at 75% more than his
efficiency. Both A and B working together can complete the work in 6
days. Find the time taken by B to complete the whole work ?
~~~~~~~~~~~~~~~~~~
This problem is on a "rate of work ".
Let x be the A's rate of work;
Let y be the B's rate of work.
The first statement "116.6% of the work done by B at 10% of his efficiency is equal to
25% of the work done by A when he work at 75% more than his efficiency"
means that
1.166*(0.1y) = 0.25*(1+0.75)x.
Also, understanding that the problem's creator wanted to say " 116.6...% " instead of 116.6%
(kind of joke from his side), we can rewrite this equation in the form
~~~~~~~~~~~~~~~~~~~~~~~~~~
1 * *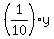 = =  ,
or ,
or
 = =  .
Reducing the factor 7 in both sides, we get .
Reducing the factor 7 in both sides, we get
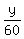 = =  , or , or  = =  , or x = , or x = 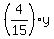 . (1)
The second statement "Both A and B working together can complete the work in 6 days"
means that
x + y = . (1)
The second statement "Both A and B working together can complete the work in 6 days"
means that
x + y =  .
Substitute here x = .
Substitute here x = 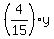 from (1), and you will get from (1), and you will get
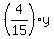 + y = + y =  ,
or ,
or
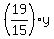 = =  , y = , y = 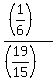 = = 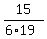 = = 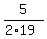 = = 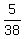 .
It means that B can complete the job in .
It means that B can complete the job in  = 7 = 7 days working alone. ANSWER days working alone. ANSWER
Solved.
/////////////////
So, this problem is partly " a joke ", but it is a bit a crocked/curved joke.
Me, from my side, tried to teach you on how to solve this problem and similar problems in a rational way.
"A rational way" in this case means "saying minimum words and writing minimum equations,
but still enough in order for everything be clear".
|
|
|