Question 1201559: hello there. can you please help me w/ this vectors hw question? it's from my "vectors as forces" lesson.
A mass of 20 kg is suspended from a ceiling by two lengths of rope that make
angles of 30° and 45° with the ceiling. Determine the tension in each of the ropes.
i tried to do it below...
30 degrees = F1
45 degrees = F2
20 x 9.8m/s^2 = 196 so 20 kg is 196N
break triangle in half;
triangle: 120 degrrees in middle, 45 on f2 side, 30 on f1 side
f1/sin45 = f2/sin30 = 196N/sin120
i'm not sure what i'm doing from here
thank you.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let T1 be the tension of the rope 30°; T2 be the tension of the rope 45°.
T1 and T2 are the magnitudes of the forces; their dimensions are newtons.
Force F1 has horizontal component T1*cos(30°) = 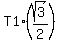 .
Force F2 has horizontal component T2*cos(45°) = .
Force F2 has horizontal component T2*cos(45°) = 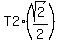 in opposite direction.
Equilibrium condition in horizontal direction gives you this equation in opposite direction.
Equilibrium condition in horizontal direction gives you this equation
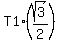 } = } = 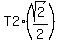 , or , or
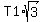 = = 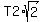 . (1)
Force F1 has vertical component T1*sin(30°) = . (1)
Force F1 has vertical component T1*sin(30°) = 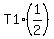 .
Force F2 has vertical component T2*sin(45°) = .
Force F2 has vertical component T2*sin(45°) = 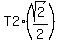 .
Equilibrium condition in vertical direction gives you this equation .
Equilibrium condition in vertical direction gives you this equation
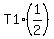 + + 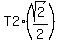 } = 20*g, or } = 20*g, or
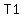 + + 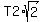 = 40g. (2)
Thus you have a system of two equations (1) and (2), and now your task is to solve it.
For it, replace in equation (2) the term = 40g. (2)
Thus you have a system of two equations (1) and (2), and now your task is to solve it.
For it, replace in equation (2) the term 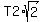 } by } by 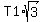 , based on equation (1).
You will get then
T1 + , based on equation (1).
You will get then
T1 + 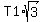 = 40g, or = 40g, or
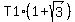 = 40g,
T1 = = 40g,
T1 = 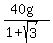 .
From equation (1), you get then
T2 = .
From equation (1), you get then
T2 = 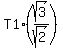 = =  .
At this point, the problem is just solved.
If you want to get the numerical values for magnitudes / (tensions) T1 and T2, use your calculator. .
At this point, the problem is just solved.
If you want to get the numerical values for magnitudes / (tensions) T1 and T2, use your calculator.
Solved.
|
|
|