Question 1201520: A student studying for a vocabulary test knows the meanings of 16 words from a list of 22 words. If the test contains 10 words from the study list, what is the probability that at least 8 of the words on the test are words that the student knows? (Round your answer to three decimal places.)
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A student studying for a vocabulary test knows the meanings of 16 words
from a list of 22 words. If the test contains 10 words from the study list,
what is the probability that at least 8 of the words on the test are words
that the student knows? (Round your answer to three decimal places.)
~~~~~~~~~~~~~~~~~~~~~~
From the study list of 22 words, the number of tests containing 10 words, is
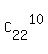 = =  = 646646.
The number of test of the length 10, of which the student knows 8 words, is = 646646.
The number of test of the length 10, of which the student knows 8 words, is
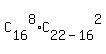 = = 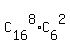 = 12870*15 = 193050. (1)
(each such test is a combination of 8 known words of 16 with 2 added unknown words of 22-16 = 6).
The number of test of the length 10, of which the student knows 9 words, is = 12870*15 = 193050. (1)
(each such test is a combination of 8 known words of 16 with 2 added unknown words of 22-16 = 6).
The number of test of the length 10, of which the student knows 9 words, is
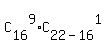 = = 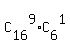 = 11440*6 = 68640. (2)
(each such test is a combination of 9 known words of 16 with 1 added unknown word of 22-16 = 6).
The number of test of the length 10, of which the student knows 10 words, is = 11440*6 = 68640. (2)
(each such test is a combination of 9 known words of 16 with 1 added unknown word of 22-16 = 6).
The number of test of the length 10, of which the student knows 10 words, is
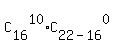 = = 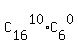 = 8008*1 = 8008. (3)
(each such test is a combination of 10 known words of 16 just without any additions).
The total number of favorable tests is the sum of the numbers (1), (2) and (3)
193050 + 68640 + 8008 = 269698.
Now the probability under the problem's question is
P = = 8008*1 = 8008. (3)
(each such test is a combination of 10 known words of 16 just without any additions).
The total number of favorable tests is the sum of the numbers (1), (2) and (3)
193050 + 68640 + 8008 = 269698.
Now the probability under the problem's question is
P = 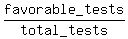 = =  = = 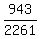 = 0.4171 (rounded). ANSWER = 0.4171 (rounded). ANSWER
Solved.
|
|
|