Question 1201504: An aquarium that holds 40 cubic meters of water is to be made such that the length of its base is twice the width. If material for the base costs $20 per square meter, and the material for the sides costs $16 per square meter, find the cost of the materials for the cheapest such aquarium.
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! An aquarium that holds 40 cubic meters of water
L*w*h = 40
is to be made such that the length of its base is twice the width.
L = 2w
therefore if we replace L with 2w
2w^2h = 40
divide eq by 2
w^2h = 20
or
h = 20/(w^2)
If material for the base costs $20 per square meter,
20(L*w)
replace L with 2w
20(2w^2 = 40w^2 is cost of the base
and the material for the sides costs $16 per square meter,
16(2(L*h)
32Lh
replace L with 2w
32(2wh) = 64wh is the cost of the long sides
and
16(2(w*h))
32wh is the cost of the shorter sides
cost of the sides:
64wh + 32wh = 96wh the total cost of the sides
find the cost of the materials for the cheapest such aquarium.
40w^2 + 96wh = total cost
replace h with 20/w^2
40w^2 + 96w(20/w^2)
multiply, cancel w
40w^2 + 1920/w = total cost
we can simplify to solve, divide by 40
w^2 + 48/w
find the minimum on your graphing calc, w=3 is minimum cost
then L = 6 is the length and h = 20/3^2 = 2.22 meters
Check: 6 * 3 * 2.22 = 40 cubic meters
:
find the cost of the materials for the cheapest such aquarium.
Base cost: 40*3^2 = 360
Long sides 64*3*2.22 = 426.24
Short sides 32*3*2.22 = 213.12
----------------------------------
total cost of aquarium 999.36 ~ $1000
:
Check using total equation
40(3^2) + 1920/3 = 1000
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An aquarium that holds 40 cubic meters of water is to be made
such that the length of its base is twice the width.
If material for the base costs $20 per square meter, and the material for the sides
costs $16 per square meter, find the cost of the materials for the cheapest such aquarium.
~~~~~~~~~~~~~~~~
Let w be the width of the aquarium;
then its length is 2w, according to the problem.
If the height is h, then the volume is
V = w*(2w)*h = 2w^2*h,
so
2w^2*h = 40 cubic meters, or
w^2*h = 20 cubic meters.
It gives h = 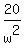 . (1)
The base area is w*(2w) = 2w^2; the base cost is 20*2w^2 = 40w^2 dollars.
The lateral area is (w + 2w + w + 2w)*h = 6wh. The lateral sides cost is 16*6wh = 96wh dollars.
The total cost is
C = 40w^2 + 96wh = substitute h from (1) = . (1)
The base area is w*(2w) = 2w^2; the base cost is 20*2w^2 = 40w^2 dollars.
The lateral area is (w + 2w + w + 2w)*h = 6wh. The lateral sides cost is 16*6wh = 96wh dollars.
The total cost is
C = 40w^2 + 96wh = substitute h from (1) = 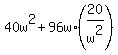 = = 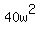 + + 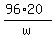 = = 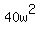 + + 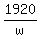 .
So, we want to minimize this function C(w) = .
So, we want to minimize this function C(w) = 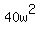 + + 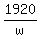 . (2)
To find the minimum, take the derivative and equate it to zero.
Doing it, you will get, step by step
80w = . (2)
To find the minimum, take the derivative and equate it to zero.
Doing it, you will get, step by step
80w = 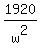 80w^3 = 1920
w^3 = 1920/80 = 24
w =
80w^3 = 1920
w^3 = 1920/80 = 24
w = 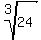 = 2.88.
Thus the width is 2.885 m; the length is twice of it 2*2.885 = 5.77 m.
the height is = 2.88.
Thus the width is 2.885 m; the length is twice of it 2*2.885 = 5.77 m.
the height is 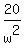 = = 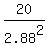 = 2.41 m.
The cheapest cost is C = formula (2) = = 2.41 m.
The cheapest cost is C = formula (2) =  + + 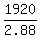 = 998.43 dollars. = 998.43 dollars.
Solved.
|
|
|