Question 1201380: Working together, two men can do a particular job in 20 days. Working alone however, it would take one man 9 days longer than the other to complete the job. Jow long would it take each man to do the job separately?
Found 3 solutions by josgarithmetic, ikleyn, math_tutor2020:
Answer by josgarithmetic(39631)   (Show Source): (Show Source):
Answer by ikleyn(52928)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Working together, two men can do a particular job in 20 days.
Working alone however, it would take one man 9 days longer than the other to complete the job.
How long would it take each man to do the job separately?
~~~~~~~~~~~~~~~~~
Let x be the number of day for the faster man to do the job alone.
Then the other man can complete the job in (x+9) days.
In one day, 1st man can do  of the entire job.
In one day, 2nd man can do of the entire job.
In one day, 2nd man can do 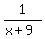 of the entire job.
Working together, they can do of the entire job.
Working together, they can do  + + 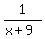 of the entire job per day.
According to the condition, this part, of the entire job per day.
According to the condition, this part,  + + 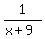 , is , is  of the job.
So you get your basic equation of the job.
So you get your basic equation
 + + 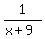 = =  . (1)
+--------------------------------------------------+
| At this point, the setup is complete, |
| and now your task is to solve this equation. |
+--------------------------------------------------+
For it, multiply both sides of equation (1) by 20x*(x+9) and simplify step by step.
20(x+9) + 20x = x*(x+9)
20x + 180 + 20x = x^2 + 9x
x^2 - 31x - 180 = 0.
Factor left side
(x+5)*(x-36) = 0
Of two roots, -5 and 36, only positive root is the solution.
Thus 1st man can complete the job in 36 days; 2nd man can complete the job in 36+9 = 45 days,
working alone.
CHECK. We check equation (1) . (1)
+--------------------------------------------------+
| At this point, the setup is complete, |
| and now your task is to solve this equation. |
+--------------------------------------------------+
For it, multiply both sides of equation (1) by 20x*(x+9) and simplify step by step.
20(x+9) + 20x = x*(x+9)
20x + 180 + 20x = x^2 + 9x
x^2 - 31x - 180 = 0.
Factor left side
(x+5)*(x-36) = 0
Of two roots, -5 and 36, only positive root is the solution.
Thus 1st man can complete the job in 36 days; 2nd man can complete the job in 36+9 = 45 days,
working alone.
CHECK. We check equation (1)
 + +  = =  = =  = =  = = 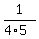 = =  .
! CORRECT ! .
! CORRECT !
Solved.
It is a typical example on how to solve similar problems.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:
Worker A = 36 days
Worker B = 45 days
=========================================================================================================================
Explanation:
Let's say the job is to move boxes from one side of a warehouse to the other.
T = total number of boxes to move
Two men can move T boxes in 20 days when working together.
We must assume they do not get in each other's way.
Their combined rate is T/20 boxes per day.
Formula:
rate = (amount done)/(time)
x = some positive whole number
x = time, in days, it takes worker A to do the job alone
x+9 = time, in days, it takes worker B to do the job alone
Worker B is the slower worker.
Here are the unit rates for each person when they work alone.
worker A's rate: T/x
worker B's rate: T/(x+9)
The sum of these unit rates must be the combined rate of T/20 boxes per day we calculated earlier.
T/x + T/(x+9) = T/20
1/x + 1/(x+9) = 1/20 .... divide both sides by T
As you can see, the total number of boxes (T) cancels out.
It turns out it doesn't matter what this total is.
The answer will be the same.




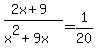





Use the quadratic formula to solve for x.
Plugging in a = 1, b = -31, c = -180





 or or 
 or or 
 or or 
Ignore the negative x value.
This is because we cannot have a negative number of days.
The only possible answer is x = 36
x = 36
x+9 = 36+9 = 45
Worker A needs 36 days to do the job alone.
Worker B needs 45 days to do the job alone.
--------------
Check:
As mentioned earlier, the total (T) doesn't matter.
Let's say we go for T = 720 boxes total.
This value is a common multiple of 36 and 45, so the next two division calculations result in a whole number.
Compute the unit rates for each worker.
Worker A: (720 boxes)/(36 days) = 20 boxes per day
Worker B: (720 boxes)/(45 days) = 16 boxes per day
Let 20 days elapse.
Worker A has moved 20*20 = 400 boxes
Worker B has moved 20*16 = 320 boxes
total moved = A+B = 400 + 320 = 720
The answer is confirmed.
Note the combined rate is 20+16 = 36 boxes per day.
After 20 days, the men have moved 36*20 = 720 boxes.
|
|
|