.
Find all zeros of the polynomial.
(Enter your answers as a comma-separated list. Enter all answers including repetitions.)
P(x) = x^4 + x^3 + 14x^2 + 16x − 32.
~~~~~~~~~~~~~~~~~
Your first move is to find the rational zeroes.
According to the Rational roots theorem, they are among the integer divisors
of the constant term -32.
So, we first check the numbers 1, 2, 4, 8, 16, 32, -1, -2, -4, -8, -16, -32
if they are the roots.
It is quite mechanical job, and doing this way, you find that 1 and -2 are the integer roots.
Hence, the given polybomial is divisible by (x-1)*(x+2) = x^2+x-2.
Performing long division, you find the quotient
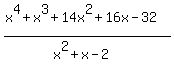= x^2 + 16.
This last polynomial (the quotient) just has no zeroes over real numbers.
It has the complex number zeroes +/- 4i.
Thus the real roots of the given polynomial are 1 and -2; the complex roots are 4i and -4i.
Solved.
