|
Question 1201150: A certain automobile cooling system contains 12.0 L of coolant that is 15% antifreeze.
How many liters of mixture must be removed so that, when it is replaced with pure antifreeze, a mixture of 23% antifreeze will result?
Found 2 solutions by ikleyn, mananth:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A certain automobile cooling system contains 12.0 L of coolant that is 15% antifreeze.
How many liters of mixture must be removed so that, when it is replaced with pure antifreeze,
a mixture of 23% antifreeze will result?
~~~~~~~~~~~~~~~~
Let x be the volume of the mixture, in liters, which should be removed and replaced
by the pure antifreeze.
Then the remaining volume of the mixture is (12-x) liters, anf it contains
0.15*(12-x) liters of the pure antifreeze.
After adding x liters of the pure antifreeze, the volume of the pure antifreeze in
the updated mixture is (0.15*(12-x)+x) liters.
The total volume of the updated mixtures remains the same 12 liters.
So, the concentration equation is
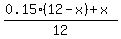 = 0.23.
Simplify and find x
0.15*(12-x) + x = 0.23*12
1.8 - 0.15x + x = 2.76
0.85x = 2.76 - 1.8
0.85x = 0.96
x = 0.96/0.85 = 1.129 liters (rounded). ANSWER
CHECK the new concentration = 0.23.
Simplify and find x
0.15*(12-x) + x = 0.23*12
1.8 - 0.15x + x = 2.76
0.85x = 2.76 - 1.8
0.85x = 0.96
x = 0.96/0.85 = 1.129 liters (rounded). ANSWER
CHECK the new concentration 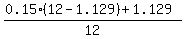 = 0.22997... (correct). = 0.22997... (correct).
Solved.
-------------------
It is a standard and typical mixture problem.
In this site, there is a bunch of lessons, covering various types of mixture problems. See introductory lessons
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions
- Word problems on mixtures for alloys
- Typical word problems on mixtures from the archive
Read them and become an expert in solution the mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A certain automobile cooling system contains 12.0 L of coolant that is 15% antifreeze.
How many liters of mixture must be removed so that, when it is replaced with pure antifreeze, a mixture of 23% antifreeze will result?
Initialquantity = 12L
strength = 15%
remove x litres
Solution remaining = (12-x)
You add pure antifreeze to replace x
Final antifreeze 23% 12 L
(12-x)*15% +100%*x = 23%*12
Multiply by 100 the equation
(12-x)*15 +100x=23*12
180-15x+100x=276
85x =96
x =96/85
=1.13 L has to be removed
|
|
|
| |