SOLUTION: In each exam question, a student receives zero, one, or two points with probabilities p0, p1, and p2 = 1 - p0 - p1, respectively. The exam consists of n questions. What is the prob

In this problem, getting (2n-2) points means loosing 2 (two) points in n answers.


Two points can be lose in two ways: EITHER two answers among n answers are 1-point answers 
(with the probability of p1) OR one answer among n answers is zero-point answer (with the probability p0).


These events are disjoint, so

    P(to lose two points) =   P(two answers of n answers are 1-point answers; the rest n-2 answers are 2-point answers) + 

                            + P(one answer is 0-point answer; the rest n-1 answers are 2-point answers) = 

                          =   + .


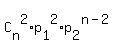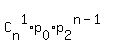For the given values, we have  = 1 - 0.36-0.15 = 0.49;  therefore

    P(to lose two points) = 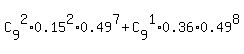 =  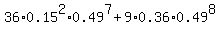= 0.016261076.   (1)



Similarly,  getting (2n-1) points means loosing 1 (one) point in n answers

    P(to lose one point) = 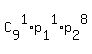 =  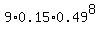= 0.004486446.    (2)



Getting 2n points means loosing nothing (same as getting (2n) two-points answers) and has the probability

    P(to lose nothing) =  =  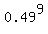= 0.001628414.    (3)



Now, tho answer the problem's question, you only need to add the numbers (1), (2) and (3)

    P = 0.016261076 + 0.004486446 + 0.001628414 = 0.02238 (rounded).