SOLUTION: you deposit $90 into an account at the beginning of each month.The bank pays you 10% interest per year compounded monthly, at the end of nine years after 108 payments, how much wil

Algebra ->  Finance -> SOLUTION: you deposit $90 into an account at the beginning of each month.The bank pays you 10% interest per year compounded monthly, at the end of nine years after 108 payments, how much wil      Log On


   

Question 1201058: you deposit $90 into an account at the beginning of each month.The bank pays you 10% interest per year compounded monthly, at the end of nine years after 108 payments, how much will my account contain?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
you will have 15,795.37442 at the end of the 9 year investment period.
here's what the yearly balances in the account look like in excel.





here's what the results look like using the financial calculator at https://arachnoid.com/finance/



payment amount is negative becauswe it's money going out.
future value is positive because it'smoney coming in.
yearly interest rate of 10% is divided by 12 to get monthly interest rate of .83333333...
payments are made at the beginning of each time period.
number of time periods are 9 years * 12 months per year = 108.

Answer by ikleyn(52866) About Me  (Show Source):
You can put this solution on YOUR website!
.
you deposit $90 into an account at the beginning of each month.
The bank pays you 10% interest per year compounded monthly, at the end of nine years.
after 108 payments, how much will highlight%28cross%28my%29%29 YOUR account contain?
~~~~~~~~~~~~~~~~~~~ 

It is a classic Annuity Due saving plan. The general formula is 


    FV = 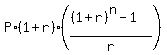P%2A%281%2Br%29%2A%28%28%281%2Br%29%5En-1%29%2Fr%29,    (1)


where  FV is the future value of the account;  P is the monthly payment (deposit) 
at the beginning of each month; r is the monthly percentage yield presented as a decimal; 
n is the number of deposits (= the number of years multiplied by 12, in this case).


Under the given conditions, P = 90 dollars;  r = 0.10/12;  n = 12*9 = 108 months.  
So, according to the formula (1), you will get at the end of the 9-th year


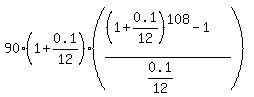    FV = 90%2A%281%2B0.1%2F12%29%2A%28%28%281%2B0.1%2F12%29%5E108-1%29%2F%280.1%2F12%29%29 = $15795.37  (rounded).


Note that you will deposit only  12*9*$90 = $9720 in 9 years.  
The rest is what the account earns/accumulates in 9 years.

-----------------

On Annuity Due saving plans,  see the lesson
    - Annuity Due saving plans and geometric progressions
in this site.

By some mysterious way, this Annuity Due saving plan has some relation to geometric progressions.

This referred lesson contains  EVERYTHING  you need to know about this subject,  in clear and compact form.

Reading it, you will learn on how it does relate to geometric progressions, too.


//////////////////


It is not for the first time this problem comes to the forum.

I just saw it once,  probably,  a month ago or so.

That time,  exactly as today,  it also came with this error  " you deposit . . . "  combined with  " how much will my account contain ".


        So,  it systematically mixes  " your deposit "  and  " my account ".


        Can you fix it in a way it would not repeated in the future ?