Question 1201032: Formulate but do not solve the problem.
The management of a private investment club has a fund of $300,000 earmarked for investment in stocks. To arrive at an acceptable overall level of risk, the stocks that management is considering have been classified into three categories: high-risk, medium-risk, and low-risk. Management estimates that high-risk stocks will have a rate of return of 16%/year; medium-risk stocks, 10%/year; and low-risk stocks, 6%/year. The investment in low-risk stocks is to be twice the sum of the investments in stocks of the other two categories. If the investment goal is to have an average rate of return of 9%/year on the total investment, determine how much the club should invest in each type of stock. (Assume that all the money available for investment is invested. Let x, y, and z denote the amount, in dollars, invested in high-, medium-, and low-risk stocks, respectively.)
? = 300,000
? = z
? = .09(300,000)
Found 2 solutions by Glaviolette, MathTherapy:
Answer by Glaviolette(140)   (Show Source):
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Formulate but do not solve the problem.
The management of a private investment club has a fund of $300,000 earmarked for investment in stocks. To arrive at an acceptable overall level of risk, the stocks that management is considering have been classified into three categories: high-risk, medium-risk, and low-risk. Management estimates that high-risk stocks will have a rate of return of 16%/year; medium-risk stocks, 10%/year; and low-risk stocks, 6%/year. The investment in low-risk stocks is to be twice the sum of the investments in stocks of the other two categories. If the investment goal is to have an average rate of return of 9%/year on the total investment, determine how much the club should invest in each type of stock. (Assume that all the money available for investment is invested. Let x, y, and z denote the amount, in dollars, invested in high-, medium-, and low-risk stocks, respectively.)
? = 300,000
? = z
? = .09(300,000)
With high, medium, and low-risk amounts being x, y, and z, respectively, we get the following equations:
x + y + z = 300,000 -- eq (i)
z = 2(x + y)____ ------- eq (ii)
.16x + .1y + .06z = .09(300,000)____.16x + .1y + .06z = 27,000 --- eq (iii)
x + y + z = 300,000 ---- eq (i)
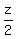 ---- Substituting  for x + y in eq (i)
z + 2z = 600,000 ----- Multiplying by LCD, 2
3z = 600,000
Amount invested in the low-risk stocks, or 
.16x + .1y + .06(200,000) = 27,000 ----- Substituting 200,000 for z in eq (iii)
.16x + .1y + 12,000 = 27,000
.16x + .1y = 15,000 ----- eq (iv)
x + y + 200,000 = 300,000____x + y = 100,000 ------ Substituting 200,000 for z in eq (i) ----- eq (v)
.1x + .1y = .1(100,000) -- Multiplying eq (v) by .1
.1x + .1y = 10,000 ---- eq (vi)
.06x = 5,000 ----- Subtracting eq (vi) from eq (iv)
Amount invested in the high-risk stocks, or 
You should now be able to determine the amount invested in the medium-risk by substituting 83,333 for y in eq (v)
|
|
|
