SOLUTION: Find the equations for each line that passes through the point (4,-1) and is tangent to the curve y=x^2+4x+3.

Algebra ->  Equations -> SOLUTION: Find the equations for each line that passes through the point (4,-1) and is tangent to the curve y=x^2+4x+3.      Log On


   

Question 1201007: Find the equations for each line that passes through the point (4,-1) and is tangent to the curve y=x^2+4x+3.
Found 2 solutions by mccravyedwin, Edwin McCravy:
Answer by mccravyedwin(406) About Me  (Show Source):
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
The equation of a line through a point (x1,y1)
with slope m is y-y%5B1%5D=m%28x-x%5B1%5D%29

The equation of every line through (4,-1) with slope m is

y-%28-1%29=m%28x-%284%29%5E%22%22%29
y%2B1=mx-4m
y=mx-4m-1

Usually if a line intersects a parabola, it intersects it in TWO points
However, a tangent line must intersect a parabola in only ONE (not TWO!)
points.  So when we solve the system of the parabola and the line:

system%28y=x%5E2%2B4x%2B3%2Cy=mx-4m-1%29

we must get only ONE solution.  We set the right sides equal:

x%5E2%2B4x%2B3=mx-4m-1
x%5E2%2B4x-mx%2B4%2B4m%2B4=0
x%5E2%2B%284-m%29x%2B%284m%2B4%29=0

To guarantee this has only ONE solution, the discriminant must be 0.

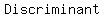
Discriminant%22%22=%22%22b%5E2-4ac, a=1, b=4-m, c=4m+4.

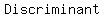
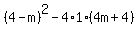
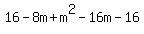
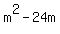Discriminant%22%22=%22%22%284-m%29%5E2-4%2A1%2A%284m%2B4%29%22%22=%22%2216-8m%2Bm%5E2-16m-16%22%22=%22%22m%5E2-24m
So we set this discriminant equal to 0:

m%5E2-24m=0
m%28m-24%29=0
m=0; m-24=0
       m=24
So the equations of the tangent lines are

y=mx-4m-1 with m=0, and m=24

y=0x-4%280%29-1 and y=24x-4%2824%29-1

y=-1 and y=24x-97   <---answers

The two green lines are the tangent lines.  The points of tangency are at the vertex of the parabola (-2,-1) and the point (10,143)



Edwin