SOLUTION: Each edge of a cube is expanding at a rate of 4 cm/s. a. How fast is the volume changing when each edge is 5 cm? b. At what rate is the surface area changing when each edge is

In this problem, you have values that are changing with respect to time and values that are changing with respect to the side of the cube.  You must be careful to treat them appropriately.



You are given  



From the properties of a cube, you have    where V is the volume of the cube in 





a.  Using the chain rule, one can write  



     Since V = 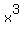,  dV/dx = 



Putting the pieces together:  dV/dt = 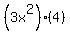 =   (cm^3/s)



   dV/dt at x=5 is:   =  300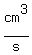 





b.  Here you can write S = 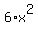  where S is the total surface area of the cube.   Follow the same procedure as above (i.e. find dS/dx and multiply by the rate of change of the sides with respect to time, i.e. 4 cm/s.  Finally, evaluate the expression at x=7.  

336