Question 1200991: A local club sells 100 tickets every week from which a winning ticket is randomly selected. Assume that every week all 100 tickets are sold and we start afresh the next week with a new lottery. If each ticket costs €3 and you buy 2 tickets every week, how much would you expect to pay overall on tickets by the time you win the lottery for the first time?
Answer by ikleyn(52813)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A local club sells 100 tickets every week from which a winning ticket is randomly selected.
Assume that every week all 100 tickets are sold and we start afresh the next week with a new lottery.
If each ticket costs €3 and you buy 2 tickets every week, how much would you expect to pay overall
on tickets by the time you win the lottery for the first time?
~~~~~~~~~~~~~~~~~~~~~
From week to week, at each lottery, we have a binomial experiment
with the probability of the success (winning at each new week/lottery) of
p = P(1st ticket wins) + P(1st ticket does not win, but the 2nd ticket wins) =
= 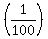 + + 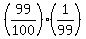 = = 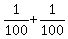 = = 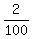 = =  = 0.02.
Repeating this experiment every week (formally, infinitely many times) and paying 2*3 = 6 euros
every week for 2 tickets, we get the mathematical expectation of the amount of the money
we pay overall on tickets by the time you win the lottery for the first time
E = 6p + 12(1-p)*p + 18(1-p)^2*p + 24(1-p)^3*p + 30(1-p)^4)*p + . . . =
= 6p*(1 + 2(1-p) + 3(1-p)^2 + 4(1-p)^3 + 5(1-p)^4 + . . . ).
The formula of the infinite sum in the brackets is classic
1 + 2*x + 3x^2 + 4x^3 + 5x^4 + . . . = = 0.02.
Repeating this experiment every week (formally, infinitely many times) and paying 2*3 = 6 euros
every week for 2 tickets, we get the mathematical expectation of the amount of the money
we pay overall on tickets by the time you win the lottery for the first time
E = 6p + 12(1-p)*p + 18(1-p)^2*p + 24(1-p)^3*p + 30(1-p)^4)*p + . . . =
= 6p*(1 + 2(1-p) + 3(1-p)^2 + 4(1-p)^3 + 5(1-p)^4 + . . . ).
The formula of the infinite sum in the brackets is classic
1 + 2*x + 3x^2 + 4x^3 + 5x^4 + . . . = 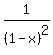 . (*)
You may find its proof everywhere (see the relevant info at the end of my post).
In our case, x = 1-p, and we get
E = . (*)
You may find its proof everywhere (see the relevant info at the end of my post).
In our case, x = 1-p, and we get
E = 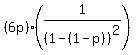 = = 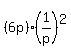 = =  = = 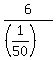 = 6*50 = 300 euros.
ANSWER. You expect to pay 300 euros overall on tickets by the time you win the lottery for the first time. = 6*50 = 300 euros.
ANSWER. You expect to pay 300 euros overall on tickets by the time you win the lottery for the first time.
Solved.
-----------------
Below is the link to the formula (*), first one, which I found in the Internet.
https://www.toppr.com/ask/en-us/question/find-the-sum-of-the-series-1-2x-3x2-4x3-dotsgiven-that/
You may find many sources for it, and, without any doubts, you may find it
in any serious textbook on combinatorics - it is like a PREREQUISITE for solving this problem.
|
|
|