Question 1200989: Please help solving bi,ii
Carter expects to live for 30 years more after his retirement. He would like to withdraw $120,000 every year from his investment account (Account A) to pay for his living expenses. Carter’s investment account (Account A) pays 5% interest per year.
How much money (a lump-sum) will Carter required to deposit in Account A at the beginning of his retirement (at age 60) to pay for his living expenses if
(i) Account A start to pay interest one year after his retirement? (5 marks) $1844694.12
(ii) Account A start to pay interest on the day of his retirement? (5 marks) $1936928.83
Continued with part (aii). Suppose Carter has just had his 35th birthday today and decided to begin his retirement (exactly) 25 years from now, at his age of 60. To ensure having sufficient funds to meet his goal, Carter plans to start depositing a fixed amount at the end of every month to a retirement savings account (Account B) that pays an interest of 12%, compounded monthly. The first deposit will be made today (on his 35th birthday) and the last on his 58th birthday.
(i) Compute the size of the monthly deposit into Account B that will allow Carter to meet the financial goal of his retirement. (8 marks)
(ii) If Carter is going to make one single (lump-sum) deposit into Account B on his 40th birthday instead, how much will that be for him to achieve the goal? (2 marks)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! he needes to have either 1844694.12 or 1936928.83 on his 60th birthday.
since he will make his last monthly deposit on his 58th birthday, then he will need to have enough money invested on his 58th birthday so that it will be equal to those sums on his 60th birthday.
his 58th birthday is 24 months before his 60th birthday.
at 1% per money rate of interest, he will need to have 1452818.61 on his 58th birthday if he needs 1844694.12 on his 60th birthday, and he need to have 1525459.54 on his 58th birthday if he needs 1936928.83 on his 60th birthday.
since he is making monthly deposite starting on his 35th birthday until his 58th birthday, he will be making 277 payments at 1% per month.
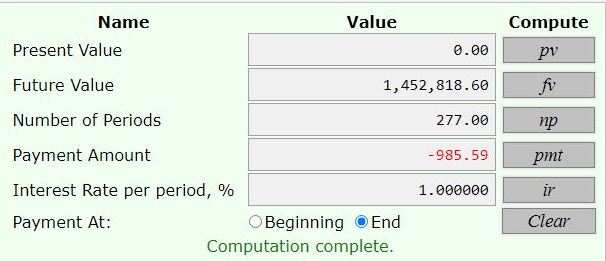
to have 1452818.61 on his 58th birthday, he will invest 985.59 at the end of each month, starting on his 35th birthday and ending on his 58th birthday.
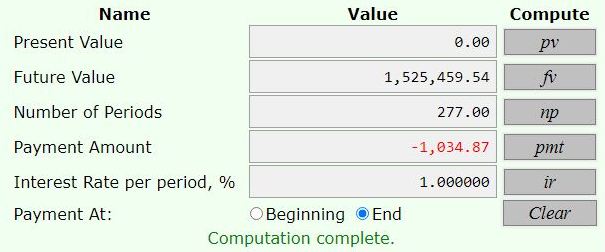
to have 2525459.54 on his 58th birthday, he will invest 1034.87 at the end of each month, strting on his 35th birthday and ending on his 58th birthday.
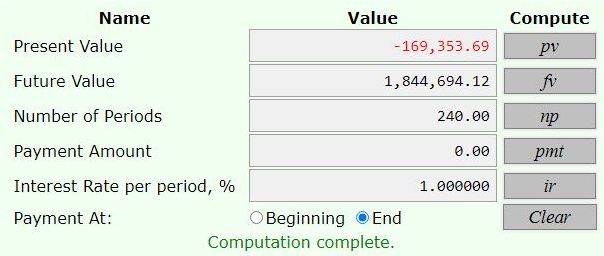
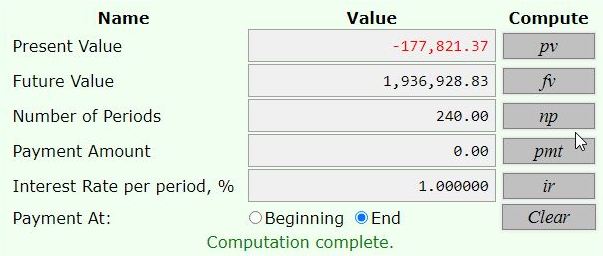
if he, instead, deposits a lump sum on his 40th birthday, then he will need to deposit 169353.69 on his 40th birthday to have 1844694.12 on his 60th birthday, or he will need to deposit 177821.37 on his 40th birthday to have 1936928.83 on his 60tbh birthday.
i used the financial calculator at https://arachnoid.com/finance/ to solve this problem.
it is an online calculator, similar in operation to the texas instruments business analyst 2 calculator which can be bought at a reasonable cost.
here are the resuts of using this calculator.
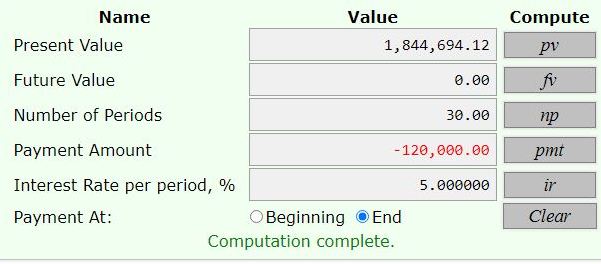
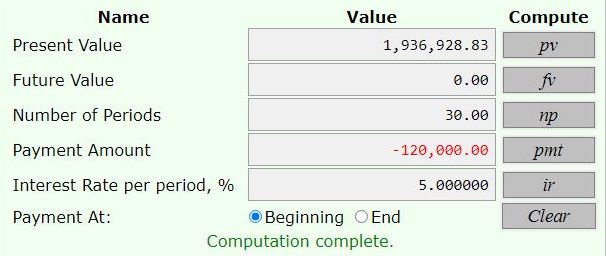
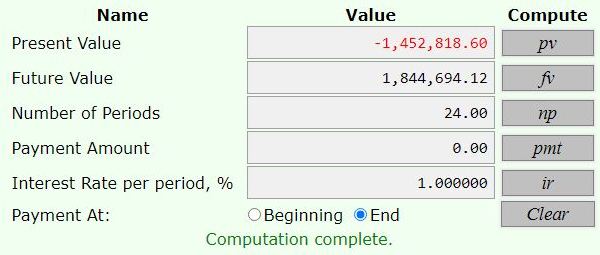
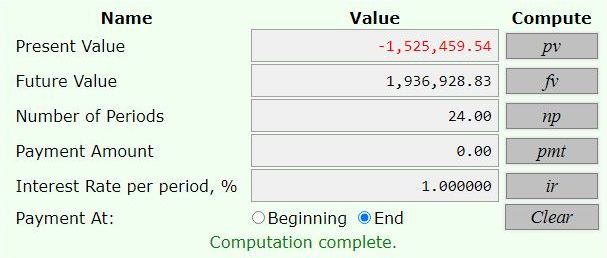
the first two were used to find how much he needed at the beginning of his retoirement period.
the annual interest rate was 5%, compounded yearly.
the next two were used to find the present value of those amount 2 years prior, when he had his 58th birthday.
the interest rate was 12% per year compounded monthly equal 1% per month.
the number of months was 24 (2 years).
the next two were used to find the monthly pament required, at thre end of each month, to get the value in the account on his 58th birthday.
the interest rate was 12% per year compounded monthly equal 1% per month.
the number of months was 277 (58 - 35 = 23 years * 12 = 276 months, plus an extra month because he was paying on his 35th birthday as well as on his 58th birthday.
normally, he would pay on his 35th birthday (payment at the beginnng of each month) or on his 58th birthday (payment at the end of each month). since there was an extra payment, i extended the period to 277 months to take that into account.
the last two looked at what he needed to invest on his 40th birthday, as a lump sum, insteadf of paying at the end of each month.
60 - 40 = 20 years * 12 = 240 months.
the rate of interest was 1% per month.
the money he required for his retirement was in account A.
the rest of the transactions were in account B.
on his 60th birthday, the money in account B was transferred to account A.
i thinks that's pretty much it.
let me know if you have any further questions.
theo
|
|
|