SOLUTION: Hi there, Hope you're doing well. Here is a question from my unit 1 (derivatives) calculus review package that I can't figure out :) Find the coordinates of the point on the

Algebra ->  Equations -> SOLUTION: Hi there, Hope you're doing well. Here is a question from my unit 1 (derivatives) calculus review package that I can't figure out :) Find the coordinates of the point on the       Log On


   

Question 1200940: Hi there,
Hope you're doing well. Here is a question from my unit 1 (derivatives) calculus review package that I can't figure out :)
Find the coordinates of the point on the curve 𝑦 = (𝑥 − 2)^2 at which the tangent line is perpendicular to the line 2𝑥 − 𝑦 + 2 = 0.
Thank you so much <3
Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!



The line  2x-y+2 = 0   can be written in  y  = mx+b  (m=slope, b=y-intercept) form:



   y = 2x + 2



By inspection, the slope is 2





A line perpendicular to a line with slope m has slope  -1/m.  So for the above line, a line perpendicular to it has slope -1/2





For the curve +y+=+%28x-2%29%5E2+  you can find the slope at any point by taking the derivative:   +dy%2Fdx+=+2%28x-2%29%2A1+ or  +dy%2Fdx+=+2x-4+

The value of the derivative dy/dx at a given x, is the the slope of the tangent of 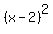+%28x-2%29%5E2+ at x.   



You are looking for x such that dy/dx = 2x - 4 = -1/2

Solving for x:  2x = -1/2 + 8/2 = 7/2  --->  x = (7/2)/2 = 7/4



At x = 7/4,  y is 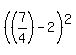+%28%287%2F4%29-2%29%5E2+ = +%28%287%2F4%29-%288%2F4%29%29%5E2+ = +%28-1%2F4%29%5E2+ =  1/16



Thus, the point  (7/4, 1/16) on  +y=%28x-2%29%5E2+ has a tangent perpendicular to the line  y = 2x + 2.



This illustrates the situation: