SOLUTION: All the real zeros of the given polynomial are integers. Find the zeros. (Enter your answers as a comma-separated list. Enter all answers including repetitions.) P(x) = x^3 −

It is an easy case of the Rational Zeroes theorem (since the leading coefficient 
of the polynomial is 1 (one)).


According to this theorem, the list of possible rational zeroes consists of these values
{1, -1, 2, -2}.


It is easy to check that x= -1 is the root.


Then the given polynomial is divisible by (x+1), so we divide the given polynomial
by (x+1) to reduce the degree

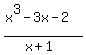     = x^2 - x - 2.


Regarding the quadratic polynomial  x^2 - x - 2, we can factor it mentally

    x^2 - x - 2 = (x-2)*(x+1).


Therefore, the final decomposition of the given polynomial is 

    x^3 − 3x − 2 = .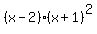


It has the roots x= 2 of multiplicity 1 and x= -1 of multiplicity 2.