.
An harbor is being attacked by 3 enemy planes.
The harbor defense system launches two missiles at each plane,
each of which independently destroys the target with a probability of 0.71.
What is the probability that at least two enemy planes will be shot down?
~~~~~~~~~~~~~~~~~~
The solution is in two steps.
First step is to determine the probability for each individual plane
to be shot down by at least one of the two missiles assigned for this plane.
This probability is P = 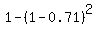 = 0.9159 (a precise value without rounding).
(1-0.71) is the probability that the target will not be destroyed by one missile;
= 0.9159 (a precise value without rounding).
(1-0.71) is the probability that the target will not be destroyed by one missile;
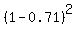 is the probability that the target will not be destroyed by two missiles;
is the probability that the target will not be destroyed by two missiles;
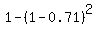 is the complement to it, meaning the probability that the target
will be destroyed by at least one of the two missiles.
is the complement to it, meaning the probability that the target
will be destroyed by at least one of the two missiles.
Second step is to solve a standard binomial distribution problem.
Now we have a standard binomial distribution probability problem.
The number of trial is n= 3; the number of success trials k is at least 2 (i.e. 2 or 3);
the probability of a success for each individual trial is 0.9159.
So, the final probability is
P = P(2) + P(3) =  =
= 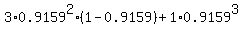 = 0.9800 (rounded). ANSWER
= 0.9800 (rounded). ANSWER
Solved in full.