SOLUTION: I have a question. How can you determine if a number is rational or irrational? 1.) Is 64 squared rational or irrational? 2.) Is -1.2 repeating decimal rational or irrati

Algebra ->  Surface-area -> SOLUTION: I have a question. How can you determine if a number is rational or irrational? 1.) Is 64 squared rational or irrational? 2.) Is -1.2 repeating decimal rational or irrati      Log On


   

Question 120076: I have a question. How can you determine if a number is rational or irrational?


1.) Is 64 squared rational or irrational?
2.) Is -1.2 repeating decimal rational or irrational?
Can some please explain different ways to determine if a number is irrational or rational? Thanks!!!!
Found 3 solutions by stanbon, Fombitz, solver91311:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
How can you determine if a number is rational or irrational?

1.) Is 64 squared rational or irrational?
Ans: Rational
----------------
2.) Is -1.2 repeating decimal rational or irrational?
Ans: Rational
-------------------
Every repeating decimal is rational.
Every non-repeating decimal is irrational.
------------------
All whole numbers are rational.
All fractions are rational.
nth roots of a^k are irrational unless k is a multiply of n.
Example: The cube root of 3^6 is rational but the cube root of 3^5 is not.
==================
Cheers,
Stan H.

Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
A rational number is a number that can be expressed as a fraction a/b where a and b are both integers (b not equal to 0, too).
64%5E2=4096 is rational because
4096=40960%2F10
1.2222222=11%2F9 so it is also rational.
Irrational numbers are numbers like
sqrt%282%29=1.41421356237...
and pi=3.141592654...
where there is no repeatable pattern.
With a repeatable pattern, then you can find the integers that make up a rational number.
0.333333333333+=+1%2F3
0.142857142857+=+1%2F7
0.11111111111+=+1%2F9
0.09099090909+=+1%2F11
0.0769230769230+=+1%2F13
and on and on.
Hope it helps.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
A rational number is one that can be expressed as the ratio (hence the name) of two integers. So if you can find any two integers p and q such that x=p%2Fq, then x is rational. Otherwise, x is irrational.

A couple of rules: Any integer is rational. That's because you can express any integer as that same integer divided by 1.

Any repeating decimal is rational, conversely, all irrational numbers are non-repeating decimals.

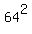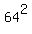Problem 1) Squaring an integer results in an integer. 64 is an integer, so 64%5E2 is an integer. All integers are rational, therefore 64%5E2 is rational.

Problem 2) All repeating decimals are rational, so -1.2... is rational. But what are the integers p and q? Hint: Any time the repeating part of the decimal is the same number, try 9 as a denominator (1%2F3=3%2F9 so the rule holds). Since the absolute value of the given number is slightly greater than 1, you need a numerator that is slightly greater than the denominator. Put the minus sign on either the numerator or the denominator. 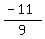%28-11%29%2F9 does quite nicely.

Here's a couple more rules for the other side of the question:

The square root of any number that is not a perfect square is irrational. The cube root of any number that is not a perfect cube is irrational. And so on...

pi, the ratio of a circle's circumference to its diameter, is irrational.

e, the base of the natural logarithms, is irrational