SOLUTION: Find the probability that when a couple has two ​children, at least one of them is a boy. ​(Assume that boys and girls are equally​ likely.)

Algebra ->  Probability-and-statistics -> SOLUTION: Find the probability that when a couple has two ​children, at least one of them is a boy. ​(Assume that boys and girls are equally​ likely.)      Log On


   

Question 1200754: Find the probability that when a couple has two ​children, at least one of them is a boy. ​(Assume that boys and girls are equally​ likely.)
Answer by ikleyn(52814) About Me  (Show Source):
You can put this solution on YOUR website!
.

The opposite (the complementary) event is "no one of two children is a boy",
i.e. both children are girl.

For this complementary event, the probability is 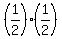 %281%2F2%29%2A%281%2F2%29 = 1%2F4.

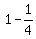Hence, for the original event under the problem's question the probability is  1+-+1%2F4 = 3%2F4.    ANSWER

Solved.


You can come to the same answer by writing and counting the events in the space of events 
    Girl Girl
    Boy  Girl
    Girl Boy
    Boy  Boy


In this table, all possible configurations are listed, and they all are equally likely.

The configurations that satisfy the problem, are ## 2, 3 and 4  of the table, 
giving the answer regarding the probability.

Solved and fully explained in two ways, for your better understanding.