Question 1200741: In an box, there are numbered balls 1, 2, ..., n. Two balls are randomly drawn without replacement. What is the probability that the sum of the numbers written on the balls will be greater than x? It is known that the number on the first ball is even. What is the probability that the sum of the numbers on the balls will be greater than x?
([n, x] = [8, 13])
Answer by ikleyn(52829)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In an box, there are numbered balls 1, 2, ..., n. Two balls are randomly drawn without replacement.
(a) What is the probability that the sum of the numbers written on the balls will be greater than x?
(b) It is known that the number on the first ball is even. What is the probability that the sum
of the numbers on the balls will be greater than x?
([n, x] = [8, 13])
~~~~~~~~~~~~~~~~~~~~~~~~
(a) In this problem, let's consider the ORDERED pairs of balls (the order of balls/numbers does matter).
The number of all possible pairs of balls (of numbers) is n*(n-1) = 8*7 = 56
with equal probability of 1/56 for each pair.
Notice that in the square matrix of the pairs/numbers, the "diagonal" pairs are EXCLUDED.
The favorable pairs are (8,7), (8,6), (6,8), (7,8) - in all, there are 4 favorable pairs.
Therefore, the probability for question (a) is  = =  . ANSWER
(b) If it is given that the number on the first ball is even, then we can consider changed/reduced both
the total set of pairs/outcomes and the set of favorable outcomes.
The total set of all possible outcomes with the even first ball/number consists of 4*7 = 28 elements (pairs).
The favorable outcomes are (8,7), (8,6), (6,8) - in all, there are 3 favorable pairs.
Therefore, the probability for question (b) is . ANSWER
(b) If it is given that the number on the first ball is even, then we can consider changed/reduced both
the total set of pairs/outcomes and the set of favorable outcomes.
The total set of all possible outcomes with the even first ball/number consists of 4*7 = 28 elements (pairs).
The favorable outcomes are (8,7), (8,6), (6,8) - in all, there are 3 favorable pairs.
Therefore, the probability for question (b) is 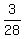 . ANSWER . ANSWER
Solved.
===================
I want to add couple of words regarding the style of presenting information in this post.
As the information is presented, it is difficult to read.
I perfectly understand that the "composer" is going to create a parametric set of problems
in order for distribute/disseminate them somewhere on some web-site changing the parameters only.
I also see that this composer takes care about his (or her) own comfort,
but does not care about the comfort of a reader, which makes me sad.
I talk about it, because I see a series of problems at this forum
(much more than one), presented in the same way.
I used to see that real problem's creators always think and care about the comfort of a reader,
on the first turn, and only after that on his or her own comfort.
|
|
|