|
Question 1200712: What is the answer to thus quadratic inequality. 3(x^2-1)>-8x. The solution should be written in interval notation.
Found 3 solutions by greenestamps, math_tutor2020, Alan3354:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) Rewrite the inequality in standard form with "0" on the right -- just as we would do if we were solving a quadratic equation:
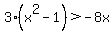 --> --> 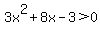
(2) Factor the quadratic expression:
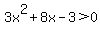 --> --> 
(3) Determine the solution set.
The expression is EQUAL to 0 at x=-3 and x=1/3. The sign of the evaluated expression can only change at those two values of x.
So, because the inequality is a strict inequality (it can't be equal to zero), we have three intervals of interest: (-infinity,-3), (-3,1/3), and (1/3,infinity). There are two basic ways to determine which of those intervals are part of the solution set.
One elementary way is to choose a test value in each of the intervals and find the intervals on which the inequality is satisfied. I will leave that to you.
Another elementary way is to know that the graph of the quadratic expression is an upward-opening parabola, so the expression is negative only between x=-3 and x=1/3. We then know on which intervals the expression is greater than zero.
ANSWER: (-infinity,-3) U (1/3,infinity)
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: (-∞, -3) U (1/3, ∞)
======================================================================
Explanation:
Let's get everything to one side
3(x^2-1) > -8x
3x^2-3 > -8x
3x^2-3 + 8x > 0
3x^2 + 8x - 3 > 0
To solve that inequality, we'll consider the corresponding equation
3x^2 + 8x - 3 = 0
We need to find the roots or x intercepts.
Factoring may or may not be possible.
The trial-and-error factoring approach is something I'm not fond of, so I prefer the quadratic formula instead.
Plug in:
a = 3
b = 8
c = -3





 or or 
 or or 
 or or 
Because each root is rational, it turns out that we could have factored previously.
The x = 1/3 leads to 3x = 1 and further leads to 3x-1 = 0
The x = -3 leads to x+3 = 0
We have the factors (3x-1) and (x+3)
Therefore, 3x^2 + 8x - 3 = (3x-1)(x+3)
You can use the FOIL rule on (3x-1)(x+3) to get 3x^2 + 8x - 3 again.
Anyways, the roots we found were:
x = -3
x = 1/3
Draw out a number line.
Mark -3 on it, and also mark 1/3
We'll label 3 regions
Region A = stuff to the left of -3
Region B = stuff between the number -3 and the number 1/3
Region C = stuff to the right of 1/3

Pick a value from region A to test.
I'll go for x = -4
3(x^2-1) > -8x
3((-4)^2-1) > -8(-4)
3(16-1) > 32
3(15) > 32
45 > 32
The final result is a true statement.
Therefore, 3(x^2-1)>-8x is true when x = -4
Furthermore, 3(x^2-1)>-8x is true for any value in region A.
We can write x < -3 as part of the solution set
Now let's test region B.
I'll use x = 0
3(x^2-1) > -8x
3(0^2-1) > -8*0
3(0-1) > 0
3(-1) > 0
-3 > 0
That is false, so region B is crossed off the list.
Lastly we need to test region C.
I'll pick x = 2.
3(x^2-1) > -8x
3(2^2-1) > -8*2
3(4-1) > -16
3(3) > -16
9 > -16
This is true, which makes x > 1/3 also part of the solution set.
Our solution set consists of x values such that
x < -3 or x > 1/3
We can rewrite x < -3 as -∞ < x < -3
We can rewrite x > 1/3 as 1/3 < x < ∞
Both of these help us get toward interval notation.
-∞ < x < -3 in interval notation is (-∞, -3)
1/3 < x < ∞ in interval notation is (1/3, ∞)
Those disjoint intervals are glued together with the union operator to arrive at the final answer of (-∞, -3) U (1/3, ∞)
This is what the solution set looks like when graphed on a number line:

Take note of the open holes at -3 and at 1/3.
Verbally we can describe the graph as having "open holes at -3 and at 1/3, with shading everywhere but between those open holes".
An alternative graph to plot is y = 3x^2+8x-3

The parabola is above the x axis when either x < -3 or when x > 1/3.
In other words, the parabola is on or below the x axis when  . Otherwise, it is above the x axis. . Otherwise, it is above the x axis.
Desmos and GeoGebra are two graphing options I recommend.
The graphing option allows a person to quickly arrive at the solution set.
However, I recommend following an algebraic approach and then use a graph to verify (rather than solely rely on a graph to do all the work for you).
A similar problem is found here
See this article for further reading.
Answer by Alan3354(69443)   (Show Source): (Show Source):
|
|
|
| |