Question 1200654: 5. The prevalence of smoking among youth in a certain country is 18%. Suppose we select six individuals from the youth
a. What is the probability that at least one is a smoker?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
Answer by ikleyn(52834)  (Show Source):
You can put this solution on YOUR website! .
The prevalence of smoking among youth in a certain country is 18%.
Suppose we select six individuals from the youth
What is the probability that at least one is a smoker?
~~~~~~~~~~~~~~~~~
For this and many other similar problems, there is another way to solve,
which is much shorter and requires less calculations (and even less knowledge).
The problem asks about "at least one person".
+------------------------------------------------------+
| In such cases, the complement is "no one person", |
| so let's calculate the probability that |
| NO ONE of 6 individuals is a smoker. |
+------------------------------------------------------+
It is P = 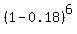 = 0.3041 (rounded).
But we need the COMPLEMENTARY probability - - - so, our answer is
P' = 1 - 0.3041 = 0.6960 (rounded).
Solved.
---------------
Thus you may know nothing about the binomial distribution;
you may know nothing about the relevant theory and formulas - nevertheless,
your intuition and your common sense will lead you to the right answer.
To see many other similar (and different) solved problems of this type, look into the lessons
- Solving probability problems using complementary probability
- Solving probability problems using complementary probability REVISITED
in this site.
Every time, when you solve a Probability problem which asks about " at least one ",
think about the complementary event " No one ".
As a rule, it is easier to calculate, and it gives you an easy and straightforward
way to get the answer. As a reward or a bonus, this way is, as a rule, more elegant.
So you earn additional scores in the eyes of other people - your friends, your classmates,
your teacher, your potential employer at the interview, or your students, if you are a teacher.
Or even in the eyes of your children or grandchildren, if you teach them at home.
At the end, I think that I will not make a mistake if I say
that this way is not only the DESIRED method of solution,
but also is the EXPECTED way to solve this problem.
|
|
|
