SOLUTION: Function h is defined by h : x —> x^2 + 4x for x ≥ k and it is given that h has an inverse. State the smallest possible value of k. Find an expression for h^-1(x).

Even though the graph of h : x —> x^2 + 4x is this parabola:



since it has a inverse, it must pass the horizontal line test.  But as you see
in the graph below, the green horizontal lines cuts the graph in two places, so
the function as graphed does not have an inverse. It is not one-to-one.

  

This is where  comes in. We must chop off enough of the graph, so
that what's left will pass the horizontal line test. We will chop it off at
the smallest value of x so that no points on the graph will be directly to the
left of any other part of the graph.  So obviously we chop it off at the very
bottom point, which is the vertex of the parabola. 

To find the vertex of a parabola we use the formula for the x-coordinate of the
vertex, which is . In the equation  "a" is the coefficient of 
x2, which is 1. The "b" is the coefficient of x, which is 4.

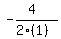
. Therefore k=-2.

So the x-coordinate of the vertex is -2, when we substitute -2 for x in
 we get the y-coordinate of the vertex . 
So the vertex is the point (-2,-4). So we chop the parabola where x=k=2, 
right at the vertex, 
so we will only leave the right half of the parabola, like this:



 
. We only use the part at or right of x=-2

To find the inverse of h(x) = x2 + 4x  for x > -2

1. We replace h(x) by y,

, 

2. We replace x by y and replace y by x:

, 

We solve for y:

, 

Multiply through by -1 to make squared term positive:

, 


Use the quadratic formula:

 







Now we work out the domain of the inverse 
Replace y by what y equals:

Add 2 to both sides

Since it is non-negative we use the positive sign
for the square root. 

That tells us that for the inverse we also use the 
positive sign for the same square root: 

Going back to the inequality, 

we square both sides. 



That's the domain of the inverse function. So the inverse is

although we write h-1(x) for y:

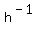
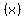
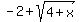
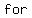
  <---ANSWER

If you want to use the same kind of notation your teacher uses,

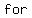
  <---ORIGINAL FUNCTION with k = -2

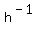
  <---INVERSE FUNCTION

Here is the graph of the inverse on the same set of axes (in blue):



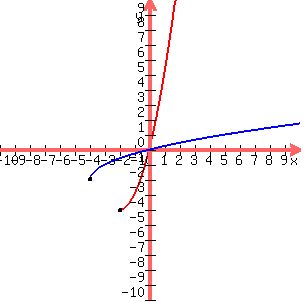And you see that the inverse is the reflection of the original function
across the identity line, whose equation is y = x  (where x and y are
identically equal and the identity line is the line that bisects the 1st and 3rd
quadrants (in green, dashed since it's not part of either graph).



Edwin