Even though the graph of h : x —> x^2 + 4x is this parabola:
 since it has a inverse, it must pass the horizontal line test. But as you see
in the graph below, the green horizontal lines cuts the graph in two places, so
the function as graphed does not have an inverse. It is not one-to-one.
since it has a inverse, it must pass the horizontal line test. But as you see
in the graph below, the green horizontal lines cuts the graph in two places, so
the function as graphed does not have an inverse. It is not one-to-one.
 This is where
This is where  comes in. We must chop off enough of the graph, so
that what's left will pass the horizontal line test. We will chop it off at
the smallest value of x so that no points on the graph will be directly to the
left of any other part of the graph. So obviously we chop it off at the very
bottom point, which is the vertex of the parabola.
To find the vertex of a parabola we use the formula for the x-coordinate of the
vertex, which is
comes in. We must chop off enough of the graph, so
that what's left will pass the horizontal line test. We will chop it off at
the smallest value of x so that no points on the graph will be directly to the
left of any other part of the graph. So obviously we chop it off at the very
bottom point, which is the vertex of the parabola.
To find the vertex of a parabola we use the formula for the x-coordinate of the
vertex, which is  . In the equation
. In the equation  "a" is the coefficient of
x2, which is 1. The "b" is the coefficient of x, which is 4.
"a" is the coefficient of
x2, which is 1. The "b" is the coefficient of x, which is 4.


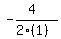

 . Therefore k=-2.
So the x-coordinate of the vertex is -2, when we substitute -2 for x in
. Therefore k=-2.
So the x-coordinate of the vertex is -2, when we substitute -2 for x in
 we get the y-coordinate of the vertex
we get the y-coordinate of the vertex 

 .
So the vertex is the point (-2,-4). So we chop the parabola where x=k=2,
right at the vertex,
so we will only leave the right half of the parabola, like this:
.
So the vertex is the point (-2,-4). So we chop the parabola where x=k=2,
right at the vertex,
so we will only leave the right half of the parabola, like this:

 . We only use the part at or right of x=-2
To find the inverse of h(x) = x2 + 4x for x > -2
1. We replace h(x) by y,
. We only use the part at or right of x=-2
To find the inverse of h(x) = x2 + 4x for x > -2
1. We replace h(x) by y,
 ,
,  2. We replace x by y and replace y by x:
2. We replace x by y and replace y by x:
 ,
,  We solve for y:
We solve for y:
 ,
,  Multiply through by -1 to make squared term positive:
Multiply through by -1 to make squared term positive:
 ,
,  Use the quadratic formula:
Use the quadratic formula:






 Now we work out the domain of the inverse
Now we work out the domain of the inverse  Replace y by what y equals:
Replace y by what y equals:
 Add 2 to both sides
Add 2 to both sides
 Since it is non-negative we use the positive sign
for the square root.
Since it is non-negative we use the positive sign
for the square root.
 That tells us that for the inverse we also use the
positive sign for the same square root:
That tells us that for the inverse we also use the
positive sign for the same square root:
 Going back to the inequality,
Going back to the inequality,
 we square both sides.
we square both sides.


 That's the domain of the inverse function. So the inverse is
That's the domain of the inverse function. So the inverse is
 although we write h-1(x) for y:
although we write h-1(x) for y:
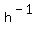
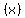

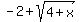
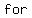
 <---ANSWER
If you want to use the same kind of notation your teacher uses,
<---ANSWER
If you want to use the same kind of notation your teacher uses,


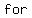
 <---ORIGINAL FUNCTION with k = -2
<---ORIGINAL FUNCTION with k = -2
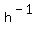

 <---INVERSE FUNCTION
Here is the graph of the inverse on the same set of axes (in blue):
<---INVERSE FUNCTION
Here is the graph of the inverse on the same set of axes (in blue):
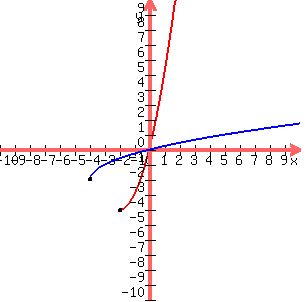 And you see that the inverse is the reflection of the original function
across the identity line, whose equation is y = x (where x and y are
identically equal and the identity line is the line that bisects the 1st and 3rd
quadrants (in green, dashed since it's not part of either graph).
And you see that the inverse is the reflection of the original function
across the identity line, whose equation is y = x (where x and y are
identically equal and the identity line is the line that bisects the 1st and 3rd
quadrants (in green, dashed since it's not part of either graph).
 Edwin
Edwin