Question 1200580: What is the number of factors of 222264 that are perfect squares?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52767)   (Show Source):
You can put this solution on YOUR website! .
What is the number of factors of 222264 that are perfect squares?
~~~~~~~~~~~~~~~~~~~~~
Prime decomposition of the number 222264 is
222264 =  .
The factors that are perfect squares are
1,  ,  ,  ,  ,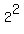
 ,  ,
 ,
 ,  ,
 ,  .
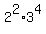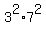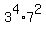In all, there are 12 factors that are perfect squares. ANSWER
Solved.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
By whatever means you want, determine that the prime factorization of 222264 is
(2^3)(3^4)(7^3)
So any factor of 222264 is of the form
(2^a)(3^b)(7^3)
where
0<=a<=3
0<=b<=4
0<=c<=3
If the factor is a perfect square, then a, b, and c all have to be even. So
a can be 0 or 2 (2 choices)
b can be 0, 2, or 4 (3 choices)
c can be 0 or 2 (2 choices)
By the fundamental counting principle, the number of factors of 222264 that are perfect squares is 2*3*2 = 12.
ANSWER: 12
|
|
|
