Question 1200577: A plane with a tailwind flew 1920 mi in 8 hours. On the return trip, against the wind, the
plane flew the same distance in 12 hours. What is the speed of the plane in calm air and
the speed of the tailwind?
Found 3 solutions by ikleyn, greenestamps, josgarithmetic:
Answer by ikleyn(52810)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A plane with a tailwind flew 1920 mi in 8 hours. On the return trip, against the wind, the
plane flew the same distance in 12 hours. What is the speed of the plane in calm air and
the speed of the tailwind?
~~~~~~~~~~~~~~~~~
The effective speed with the wind is 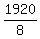 = 240 miles per hour.
The effective speed against the wind is = 240 miles per hour.
The effective speed against the wind is 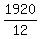 = 160 miles per hour.
In other words,
u + v = 240
u - v = 160,
where u is the speed of the aircraft in still air and v is the speed of the wind.
To solve equations, add them. You will get
2u = 240 + 160 = 400, u = 400/2 = 200.
Then from the very first equation
v = 240 - u = 40.
ANSWER. The speed of the airplane in still air is 200 miles per hour.
The speed of the wind is 40 miles per hour. = 160 miles per hour.
In other words,
u + v = 240
u - v = 160,
where u is the speed of the aircraft in still air and v is the speed of the wind.
To solve equations, add them. You will get
2u = 240 + 160 = 400, u = 400/2 = 200.
Then from the very first equation
v = 240 - u = 40.
ANSWER. The speed of the airplane in still air is 200 miles per hour.
The speed of the wind is 40 miles per hour.
Solved.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This kind of problem is encountered so often that it is useful to learn a quick way to find the answer informally -- as long as formal algebra is not required.
After determining that the speeds with and against the wind are 240 and 160 miles per hour, logical reasoning tells you that the 240mph is the plane speed plus the wind speed and the 160mph is the plane speed minus the wind speed -- and that means the plane speed is halfway between 160mph and 240mph: 200mph. And then the wind speed is the difference between 240mph and 200mph (or between 160mph and 200mph).
ANSWERS (informally): plane speed 200mph; wind speed 40mph
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
|
|
|