|
Question 1200567: A collection of nickels, dimes, and quarters is retrieved from a vending machine. There are three times as many nickels as dimes, and there are ten more quarters than dimes. If the total value of the coins is $40.00 then find the number of each type of coin.
Found 3 solutions by josgarithmetic, math_tutor2020, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
Answers:
225 nickels
75 dimes
85 quarters
Work Shown:
d = number of dimes
3d = number of nickels
d+10 = number of quarters
10d = value of the dimes (cents)
5(3d) = 15d = value of the nickels (cents)
25(d+10) = 25d+250 = value of the quarters (cents)
10d+15d+(25d+250) = 4000 cents aka $40
50d+250 = 4000
50d = 4000-250
50d = 3750
d = 3750/50
d = 75 dimes
3d = 3*75 = 225 nickels
d+10 = 75+10 = 85 quarters
Check:
225 nickels = 225*5 = 1125 cents = $11.25
75 dimes = 75*10 = 750 cents = $7.50
85 quarters = 85*25 = 2125 cents = $21.25
total = $11.25+$7.50+$21.25 = $40
The answers are confirmed.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
A collection of nickels, dimes, and quarters is retrieved from a vending machine.
There are three times as many nickels as dimes, and there are ten more quarters than dimes.
If the total value of the coins is $40.00 then find the number of each type of coin.
~~~~~~~~~~~~~~~~~
It may seem fantastic, but the problem can be
solved mentally, without using equations.
Take 10 quarters aside, for a minute.
Then the updated collection has three times as many nickels as dimes,
and the same number of quarters as dimes and it is worth
40.00 - 10*0.25 = 40 - 2.50 = 37.50 dollars.
Now group the coins in the sets, combining 1 dime, three nickels and 1 quarter in each set.
According to the problem, it CAN BE DONE.
Each set is worth 10 + 3*5 + 25 = 50 cents; so, the number of sets is 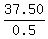 = 75.
From this, we conclude that the original collection has
75 dimes, 3*75 = 225 nickels and 75+10 = 85 quarters. ANSWER
Solved.
---------------
Good problem for a school Math circle to give it to advanced students
and ask them to solve it MENTALLY, without using equations.
////////////////////
If a Math teacher wants to bring up students with vivid mind, he (or she)
should give them such assignments from time to time.
|
|
|
| |
