Question 1200476: A piggy bank contains only nickels, dimes, and quarters. If there are 76 coins worth $8.50, and there are twice as many dimes as nickels, how many of each coin are there?
Show all of your work.
Found 3 solutions by josgarithmetic, math_tutor2020, ikleyn:
Answer by josgarithmetic(39616)   (Show Source):
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
Answer: 21 nickels, 42 dimes, 13 quarters
Work Shown:
n = number of nickels
d = number of dimes
q = number of quarters
n+d+q = 76 coins total
5n+10d+25q = 850 cents in total value
d = 2n since there are twice as many dimes as nickels
Applying substitution and solving for q.
n+d+q = 76
n+2n+q = 76 ... plug in d = 2n
3n+q = 76
q = 76-3n
Also,
5n+10d+25q = 850
5n+10(2n)+25q = 850 ... plug in d = 2n
5n+20n+25q = 850
25n+25q = 850
25(n+q) = 850
n+q = 850/25
n+q = 34
n+76-3n = 34 ... plug in q = 76-3n; solve for n
-2n+76 = 34
-2n = 34-76
-2n = -42
n = -42/(-2)
n = 21
Use that value to find the others.
d = 2n = 2*21 = 42
q = 76-3n = 76-3*21 = 76-63 = 13
In summary,
n = 21
d = 42
q = 13
to represent the number of nickels, dimes, and quarters respectively.
Check:- Coin count: 21 nickels + 42 dimes + 13 quarters = 21+42+13 = 76 coins total
- Coin value: 21 nickels + 42 dimes + 13 quarters = 21*5 + 42*10 + 13*25 = 850 cents = $8.50 total value
- The number of dimes (42) is double that of the number of nickels (21).
The answers have been confirmed.
Confirmation using WolframAlpha
https://www.wolframalpha.com/input?i=n%2Bd%2Bq+%3D+76%2C5n%2B10d%2B25q%3D850%2Cd%3D2n
The CAS mode in GeoGebra has a similar solver feature.
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
A piggy bank contains only nickels, dimes, and quarters.
If there are 76 coins worth $8.50, and there are twice as many dimes as nickels,
how many of each coin are there?
Show all of your work.
~~~~~~~~~~~~~~~~~~~~
It is a typical problem to be solved by reduction
to one single equation in one single unknown.
See how simple the solution is.
Let x be the number of nickels.
Then the number of dimes is 2x,
and the number of quarters is (76 - x - 2x) = (76-3x).
Now write the total money equation
5x + 10*(2x) + 25*(76-3x) = 850 cents.
Simplify and find x
5x + 20x + 25*76 - 25*(3x) = 850
5x + 20x + 1900 - 75x = 850
-50x = 850 - 1900
-50x = -1050
x =  =  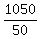=  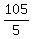= 21.
ANSWER. 21 nickels, 2*21 = 42 dimes, and the rest of coins, 76-21-42 = 13, are quarters.
CHECK. Total cents is 21*5 + 42*10 + 13*25 = 850, correct.
Solved.
--------------------
From the first glance, this problem is for 3 unknowns.
But, actually, it can be solved using only one unknown and one single equation.
There is no need to explain that obvious fact that it reduces the volume of calculations,
reduces your efforts and diminish the chances to make errors.
In addition, it is a good style to solve the problem in this way.
Therefore, from my post learn how to do it.
You also should learn to recognize such problems from the first glance.
At this site, there is a SPECIAL LESSON explaining and showing different similar problems solved in the same way
- Advanced word problems to solve using a single linear equation
Remember, that your task is not simply to get a correct answer, only.
Your task is to do it in a right way ( ! )
Happy learning ( ! )
|
|
|
