SOLUTION: The cable of suspension bridge hangs in the shape of a parabola. The towers supporting the cable are 400 ft apart and 150 ft high. If the cable, at its lowest is 30 ft above the br

If we place the origin of the coordinate system at the bridge level midpoint 
between the two towers, we have the vertex of the parabola at the point (0,30).


So, we write an equation of the parabola in vertex form

    y = ax^2 + 30.


Coefficient "a" is unknown.  It is the only unknown in this problem now.


To find it, we use the condition at the endpoint:  y= 150  at  x= 400/2 = 200.  It gives

    150 = a*200^2 + 30

    150 - 30 = a*40000

       120   = 40000a

        a   =  =  = .


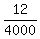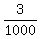Thus the parabola is  y = .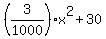    


To find the level of the cable at 50 ft from the tower, we substitute x = 200-50 = 150 ft
into the equation of the parabola. 
This way we get the height of the cable at the point x= 150 ft, which is 50 feet from the tower

    y = 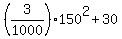 = 97.5 ft.    ANSWER

The maximum difference of the levels of the cable is 150 - 30 = 120 ft.

The distance 150 ft from the central point to the tower is  =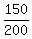 
of the half the bridge length.


Hence, the level of the cable at x= 150 ft from the center is

    30 + 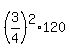 = 30 +  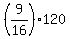= 30 +  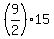= 30 + 9*7.5 = use your calculator = 97.5 ft,

giving the same answer.