SOLUTION: A cement truck delivers mixed cement to a large construction site. Let x represent the cycle time in minutes for the truck to leave the construction site, go back to the cement pla

This question is about conditional probability.

We have an event A = { x > 60 } and an event B = { x > 50 }.


They want you calculate the conditional probability P(A | B), which reads " P of A given B".


This conditional probability is the ratio  .


Here P(A and B) is the probability of the intersection (A and B).

In this problem, OBVIOUSLY, event A is a part of the event B: indeed, if x > 60, then x > 50.


Therefore, P(A and B) = P(A)    <<<---=== exactly because A is a smaller part of B.


So, our conditional probability  P(A | B) is the ratio  P(A | B) = .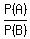


    +---------------------------------------------------------------------+
    |    As soon as we got this understanding, we solved more than half   |
    |         of the problem, and the rest is just a technique.           |
    +---------------------------------------------------------------------+


Mow,   P(A) = normalcdf(60, 9999, 48, 18)  (it is the area under the normal curve 
                                           on the right of the raw mark x=60),

  so,  using your calculator, you get the value  P(A) = 0.2525.



Next,  P(B) = normalcdf(50, 9999, 48, 18)  (it is the area under the normal curve 
                                           on the right of the raw mark x=50),

  so,  using your calculator, you get the value  P(B) = 0.4558.


Finally, the desired conditional probability is  

         P(A | B) = 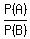 =  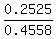= 0.5540  (rounded).    ANSWER