Question 1200106: Find all horizontal and vertical asymptotes of the function: f(x) = x/sqrt(x^2-1)
Found 2 solutions by Edwin McCravy, greenestamps:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
  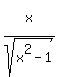 To find vertical asymptotes, set the denominator equal to 0:
To find vertical asymptotes, set the denominator equal to 0:
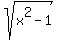  
  
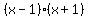   x-1 = 0; x+1 = 0
x = 1; x = -1
So the vertical asymptotes are the vertical lines whose equations are
x = 1 and x = -1
To find the horizontal asymptotes we substitute large positive and negative
numbers for x, and see if they approach any finite number.
Substituting x = 1000,
x-1 = 0; x+1 = 0
x = 1; x = -1
So the vertical asymptotes are the vertical lines whose equations are
x = 1 and x = -1
To find the horizontal asymptotes we substitute large positive and negative
numbers for x, and see if they approach any finite number.
Substituting x = 1000,
  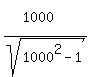  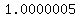 That is very close to 1, so we assume y = 1 is a horizontal asymptote.
Substituting x = -1000,
That is very close to 1, so we assume y = 1 is a horizontal asymptote.
Substituting x = -1000,
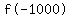  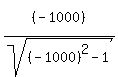  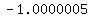 That is very close to -1, so we assume y = -1 is also a horizontal asymptote.
So we draw the vertical asymptotes x = 1 and x= -1 and horizontal asymptotes
are y = 1 and y = -1
That is very close to -1, so we assume y = -1 is also a horizontal asymptote.
So we draw the vertical asymptotes x = 1 and x= -1 and horizontal asymptotes
are y = 1 and y = -1
 Since the function contains a square root, we must ensure that what's under the
square root is greater than 0.
Since the function contains a square root, we must ensure that what's under the
square root is greater than 0.

 They have zeros 1 and -1. We make a number line
----------o-----o---------
-4 -3 -2 -1 0 1 2 3 4
Choose test point x=-2 in interval
They have zeros 1 and -1. We make a number line
----------o-----o---------
-4 -3 -2 -1 0 1 2 3 4
Choose test point x=-2 in interval 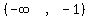



 That is a true inequality, so
That is a true inequality, so 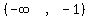 is part of
the domain.
Choose test point x=0 in interval is part of
the domain.
Choose test point x=0 in interval 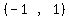



 That is a false inequality, so
That is a false inequality, so 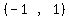 is NOT part of
the domain. Therefore there is no graph between where x=-1 and where x=1.
Choose test point x=2 in interval is NOT part of
the domain. Therefore there is no graph between where x=-1 and where x=1.
Choose test point x=2 in interval 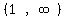



 That is a true inequality, so
That is a true inequality, so 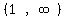 is part of
the domain. So the shaded number line is
<==========o-----o=========>
-4 -3 -2 -1 0 1 2 3 4
So the domain is is part of
the domain. So the shaded number line is
<==========o-----o=========>
-4 -3 -2 -1 0 1 2 3 4
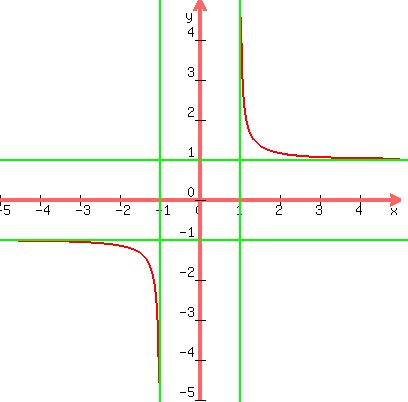
So the domain is  We find a couple points in both parts of the domain, say the points
(-2,-1.2) and (2,1.2). Then sketch the graph:
We find a couple points in both parts of the domain, say the points
(-2,-1.2) and (2,1.2). Then sketch the graph:
 Edwin
Edwin
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The denominator is 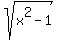 , so the radicand , so the radicand  must be non-negative. must be non-negative.
Furthermore, since that square root is in the denominator,the radicand can't be zero.
 , so the function is undefined on [-1,1]. , so the function is undefined on [-1,1].
For x values a tiny bit greater than 1, the denominator is close to 0, and the numerator is positive, so the function value is large positive. That makes x=1 a vertical asymptote.
Similarly, for x values a tiny bit less than -1, the denominator is close to 0, and here the numerator is negative, so the function value is large negative. So x=-1 is also a vertical asymptote.
For either large positive or large negative values of x, 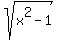 is very close to is very close to  , so the function is very nearly equal to , so the function is very nearly equal to 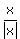 . .
For large positive values of x,  , so y=1 is a horizontal asymptote for x>1. , so y=1 is a horizontal asymptote for x>1.
For large negative values of x,  , so y=-1 is a horizontal asymptote for x<-1. , so y=-1 is a horizontal asymptote for x<-1.
ANSWERS:
vertical asymptotes at x=-1 and x=1;
horizontal asymptotes at y=1 (for positive x values) and y=-1 (for negative x values).
A graph of the function and the two horizontal asymptotes....

|
|
|