.
Find the domain of the function f(x) = ln ((x+3)/(x-2))
~~~~~~~~~~~~~~~~
The argument under the logarithm must be positive
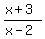 > 0.
So, there are two cases:
(a) either x+3 > 0 and x-2 > 0
(b) or x+3 < 0 and x-2 < 0.
In case (a), x > -3 and x > 2, which implies x > 2.
In case (b), x < -3 and x < 2, which implies x < -3.
ANSWER. The domain of the function
> 0.
So, there are two cases:
(a) either x+3 > 0 and x-2 > 0
(b) or x+3 < 0 and x-2 < 0.
In case (a), x > -3 and x > 2, which implies x > 2.
In case (b), x < -3 and x < 2, which implies x < -3.
ANSWER. The domain of the function 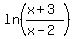 is the union of two sets (-oo,-3) U (2,oo).
is the union of two sets (-oo,-3) U (2,oo).
Solved.