SOLUTION: Find the domain of h(x) = √((x-6)/(x+1))

Algebra ->  Rational-functions -> SOLUTION: Find the domain of h(x) = √((x-6)/(x+1))      Log On


   

Question 1199851: Find the domain of h(x) = √((x-6)/(x+1))
Found 2 solutions by Edwin McCravy, math_tutor2020:
Answer by Edwin McCravy(20066) About Me  (Show Source):
You can put this solution on YOUR website!
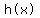%22h%28x%29%22%22%22=%22%22sqrt%28%28x-6%29%2F%28x%2B1%29%29

1. The denominator cannot be 0
   x+1 ≠ 0
     x ≠ -1

2. (x-6)/(x+1) cannot be negative. That is, either both numerator AND
denominator are both positive OR they are both negative:

[x-6 > 0 AND x+1 > 0] OR [x-6 < 0 AND x+1 > 0]
   x > 6 AND   x > -1 OR    x < 6 AND   x < -1  

When x > 6, then x > -1 is implied, redundant, and may be eliminated.
When x < -1, then x < 6 is implied, redundant, and may be eliminated.
When x < -1, then x ≠ -1 is implied, redundant, and may be eliminated.

Thus, the domain is { x | x < -1 or x > 6 }

In interval notation the domain is

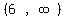%28matrix%281%2C3%2C-infinity%2C+%22%2C%22+%2C-1%29%29U%28matrix%281%2C3%2C6%2C+%22%2C%22+%2Cinfinity%29%29  

Edwin

Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

If x = -1, then the denominator x+1 is zero.
Dividing by zero is NOT allowed. We must remove x = -1 from the domain.
In other words, x+%3C%3E+-1

The stuff under the square root is known as the radicand.
The radicand cannot be negative assuming you are currently studying real-valued functions only (ie. you have yet to study complex numbers)

So we want %28x-6%29%2F%28x%2B1%29 to be nonnegative.
Symbolically we write %28x-6%29%2F%28x%2B1%29+%3E=+0


Draw out a number line with -1 and 6 marked on it.
Sub-divide the number line into 3 non-overlapping regions
  • Region A consists of stuff to the left of -1
  • Region B consists of stuff between -1 and 6
  • Region C consists of stuff to the right of 6
Pick a random value from region A.
Let's go with x = -2
%28x-6%29%2F%28x%2B1%29=%28-2-6%29%2F%28-2%2B1%29+=+%28-8%29%2F%28-1%29+=+8
The actual value doesn't matter. All we care about is whether it's positive or negative.
We got a positive result when x = -2
Thus any x value inside region A results in a positive radicand.
Furthermore, it means anything inside region A is part of the domain.

Pick a random value from region B.
Let's go with x = 0
%28x-6%29%2F%28x%2B1%29=%280-6%29%2F%280%2B1%29+=+%28-6%29%2F1+=+-6
Any x value inside region B results in a negative radicand.
Stuff in region B is NOT in the domain.

Pick a random value from region C.
Let's go with x = 7
%28x-6%29%2F%28x%2B1%29=%287-6%29%2F%287%2B1%29+=+1%2F8+=+0.125
Again the actual value doesn't matter. We only care about the sign.
We got a positive result so any x value inside region C results in a positive radicand.
In short, anything in region C is also part of the domain.

Summary table
RegionIntervalSign of (x-6)/(x+1)
A-infinity < x < -1positive
B-1 < x < 6negative
C6 < x < infinitypositive

I recommend drawing out the sign chart number line.

We see that regions A and C make (x-6)/(x+1) positive
So the domain is the set of x values that either x < -1 or x > 6
But wait: we can plug in x = 6 since it causes h(x) to be zero.
The numerator can be zero.

So we should update the domain to be x+%3C+-1 or x+%3E=+6

The interval notation would be (-infinity, -1) U [6, infinity)
The square bracket is to include the endpoint "6"
Curved parenthesis exclude the endpoint
Always use a curved parenthesis with either infinity.

Graph:
graph%28400%2C400%2C-8%2C8%2C-5%2C5%2C-100%2Csqrt%28%28x-6%29%2F%28x%2B1%29%29%29
The left branch approaches the vertical asymptote x = -1. It never reaches this value.
The gap between branches is due to the work shown in region B (see above).
There is a closed filled in endpoint at (6,0) which is the only x intercept.
There are no y intercepts.

Graphing tools such as Desmos and GeoGebra are very useful as quick visual verification methods.