|
Question 1199777: A circle passes through the vertices of a triangle with sides of length 3.3 cm, 5.6 cm and 6.5 cm. The radius of the circle, in cm, is
a) 2.3
b) 3.2
c) 3.25
d) 3.85
e) 5.16666...
Answer by ikleyn(52816)   (Show Source):
You can put this solution on YOUR website! .
A circle passes through the vertices of a triangle with sides of length 3.3 cm, 5.6 cm and 6.5 cm.
The radius of the circle, in cm, is
a) 2.3
b) 3.2
c) 3.25
d) 3.85
e) 5.16666...
~~~~~~~~~~~~~~~
There is a remarkable formula for the radius R of the circle circumscribed around
a triangle, when the sides of a triangle "a", "b" and "c" are given. This formula is
R =  ,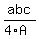
where A is the triangle area. For this formula, see the lesson
- Proof of the formula for the radius of the circumscribed circle
in this site, with the proof.
In this formula, "A" is the area of the triangle, which you can compute using the Heron's formula
A =  , (2)
where s is the semi-perimeter of a triangle.
So, calculate the area of the given triangle using the Heron's formula (2).
The area is 9.24 cm^2.
Then apply formula (1) and get
R =  = 3.25.
ANSER. The radius of the circumscribed circle is 3.25 cm.
Solved.
------------------
On the Heron's formula for the area of a triangle, see the lessons
- Proof of the Heron's formula for the area of a triangle
- One more proof of the Heron's formula for the area of a triangle
in this site.
///////////////////
Notice that the side of the triangle 6.5 cm, which is given, is precisely twice the length of the radius
of the circumscribed circle, which we computed.
It means that the given triangle is a right-angled triangle.
Indeed, you may check it on your own that 33, 56 and 65 is a Pythagorean triple.
See, how much did you learn from my post (!)
Come again to this forum soon to learn something new, useful and interesting (!)
|
|
|
| |
